机器学习考试总结
导论
机器学习能做什么
- 手写字符识别
- 汽车自动驾驶
- 下棋
- How Old Are You
什么是机器学习
-
A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E.
- 让计算机程序发现数据中的规律,并根据规律给出预测的一种智能技术
- 在大型数据库中的应用称为数据挖掘(或 KDD ),在近年叫大数据
经典的机器学习算法分类及有什么
- 分类:将事物按照标准分成一些类别
- 回归:由过去、现在的数据预测未来的状态
- 聚类:没有类别的标准,按照事物间的相似性划分成一些类别
- 增强学习
线性回归
Applications(Task) and Model
- 用途:定价、资信、物质成分浓度
- 身高回归
- 房屋资产定价
Model Representation
$h_{\theta}=\theta_{0}+\theta_{1}x$
Cost Functions of Task
$J(\theta_{0},\theta_{1})=\frac{1}{2m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})^{2}$
Optimization
求导法
\[J(\theta) =\frac{1}{2m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})^{2} \\ \frac{\partial J(\theta)}{\partial \theta_{j}} = \frac{\partial}{\partial \theta_j} \frac{1}{2m}\sum_{i=1}^m (h_{\theta}(\boldsymbol x^{(i)}) - y^{(i)})^2 \\ \frac{\partial J(\theta)}{\partial \theta_{j}} = \frac{1}{m} \sum_{i=1}^m (h_{\theta}(\boldsymbol x^{(i)}) - y^{(i)}) \frac{\partial}{\partial \theta_j}(h_{\theta}(\boldsymbol x^{(i)}) - y^{(i)}) \\ \frac{\partial J(\theta)}{\partial \theta_{j}} = \frac{1}{m} \sum_{i=1}^m (h_{\theta}(\boldsymbol x^{(i)}) - y^{(i)})x_j^{(i)} \\ \sum_{i=0}^{m}\sum_{k=0}^{n}\theta_kx_k^{(i)}x_{j}^{(i)}=\sum_{i=1}^{m}(x_j^{(i)}y^{(i)})\]使用向量表示: \(X^TX\theta=X^Ty \\ \theta=(X^TX)^{-1}X^Ty\)
梯度下降
\[repeat\text{ }until\text{ }convergence \\ \theta_0:=\theta_0-\alpha\frac{1}{m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)}) \\ \theta_1:=\theta_1-\alpha\frac{1}{m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})x^{(i)}\]Ridge Regression & LASSO
Logistic Regression
Task and Dataset
Decision Model
$h_{\theta}(\boldsymbol x)=g(\boldsymbol{\theta^Tx})=\frac{1}{1+e^{- \boldsymbol \theta^Tx} }$
决策边界:$\theta^Tx=0$
Loss Function
- $J(\theta)=\frac{1}{m}\sum_{i=1}^{m}[y^{(i)}log h_{\theta}(x^{(i)})+(1-y^{(i)})log (1-h_{\theta}(x^{(i)}))]$
-
信息熵:$CrossEntropy(P, Q)=\sum_{k=1}^{ Y }p_klog_2\frac{1}{q_k}$
Optimization
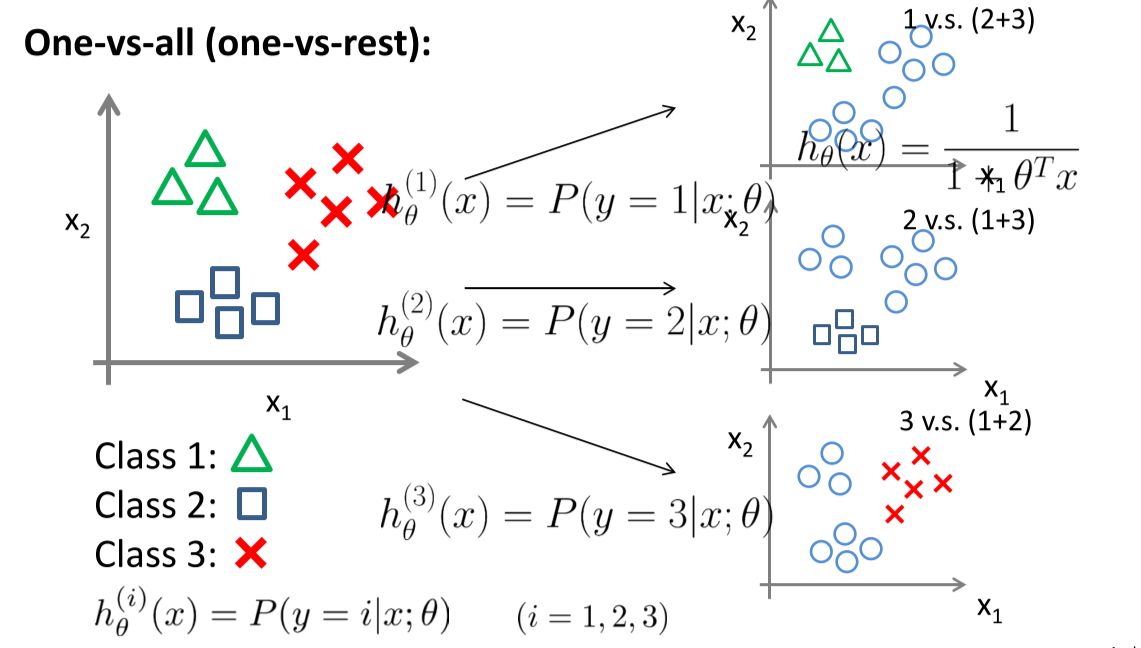
\[\begin{aligned} \frac{\partial h_{\theta}(x)}{\partial \theta} &= \frac{\part}{\part\theta}\frac{1}{1+e^{-\theta x}} \\ &= -\frac{1}{(1+e^{-\theta x})^2} \frac{\part}{\part\theta}(1+e^{-\theta x}) \\ &= -\frac{1}{(1+e^{-\theta x})^2} e^{-\theta x} (-x) \\ &= \frac{1}{(1+e^{-\theta x})} \frac{e^{-\theta x}}{1+e^{-\theta x}} x \\ &= h_{\theta}(x)(1-h_{\theta}(x))x \\ \end{aligned} \\ \begin{aligned} \frac{\partial J(\boldsymbol \theta)}{\partial \theta_j} &= \frac{1}{mln2}\sum_{i=1}^{m}[(\frac{y^{(i)}}{h_\theta(x^{(i)})}-\frac{1-y^{(i)}}{1-h_\theta(x^{(i)})}) \frac{\part}{\part \theta_j} h_\theta(x^{(i)})] \\ &=\frac{1}{m \ln 2} \sum_{i=1}^{m}\left(y^{(i)}-h\left(x^{(i)}\right)\right) x^{(i)} \end{aligned} \\\]多类分类
- 邮件标注
- 药物
- 天气分类
方法:one vs all
Linear Discriminate Analysis
核心思想:超平面切分平面,使类内距最小,类间距最大
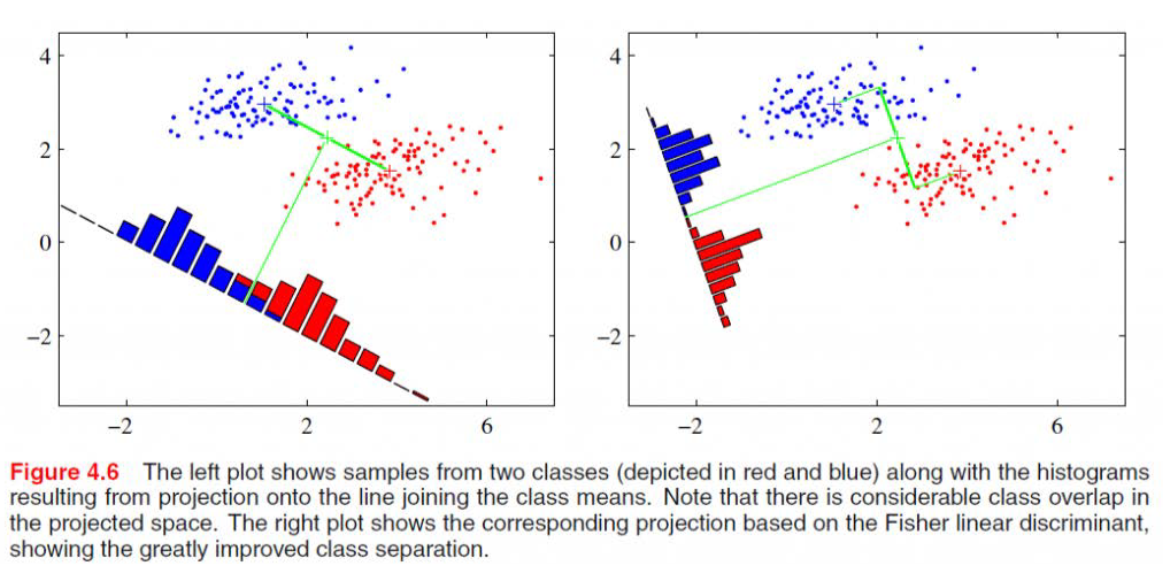
给定训练样本集合 $D={(\boldsymbol x_i,y_i)} i=1…m,y_i=1or0$
$\mu_0,\mu_1$ 分别为两类样本的均值
$\Sigma_0, \Sigma_1$ 分别为两类样本的协方差矩阵
$w^T\mu_0, w^T\mu_1$ 分别是两类样本中心在 $w$ 上的投影
$w^{T} \Sigma_{0} w, w^{T} \Sigma_{1} w$ 分别是两类样本中心在 $w$ 上的投影长度的协方差
最大类间距:$\max \left|w^{T} \mu_{0}-w^{T} \mu_{1}\right|_{2}^{2}$
最小类内距:$\min \left{w^{T} \Sigma_{0} w+w^{T} \Sigma_{1} w\right}$
Neural Network
神经元、神经网络的表示
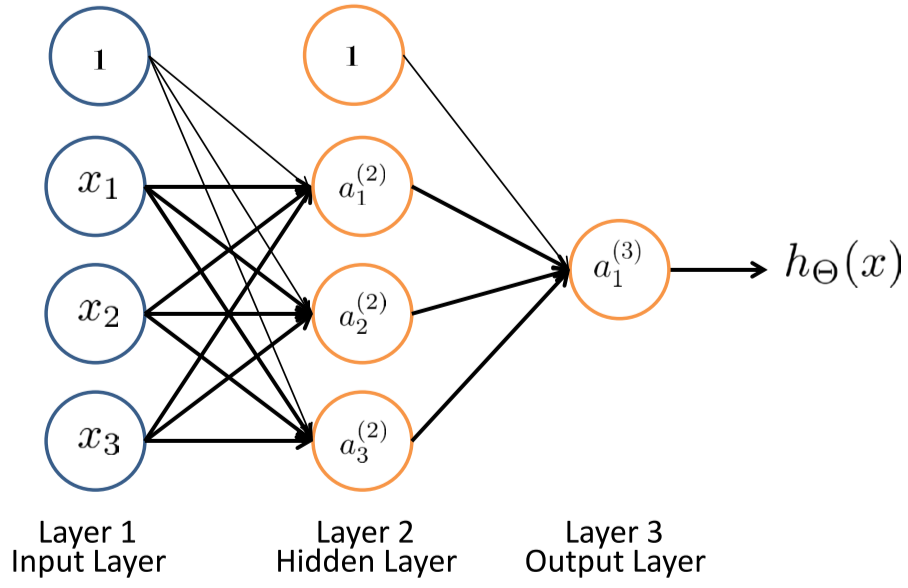
- 万能近似定理:一个前馈神经网络如果具有线性输出层和至少一层具有一种任何挤压性质的激活函数的隐藏层,只要给予网络足够数量的隐藏单元,它可以以任意精度来近似任何一个有限维空间到另一个有限维空间的Borel可测函数。
使用神经元模型实现逻辑运算
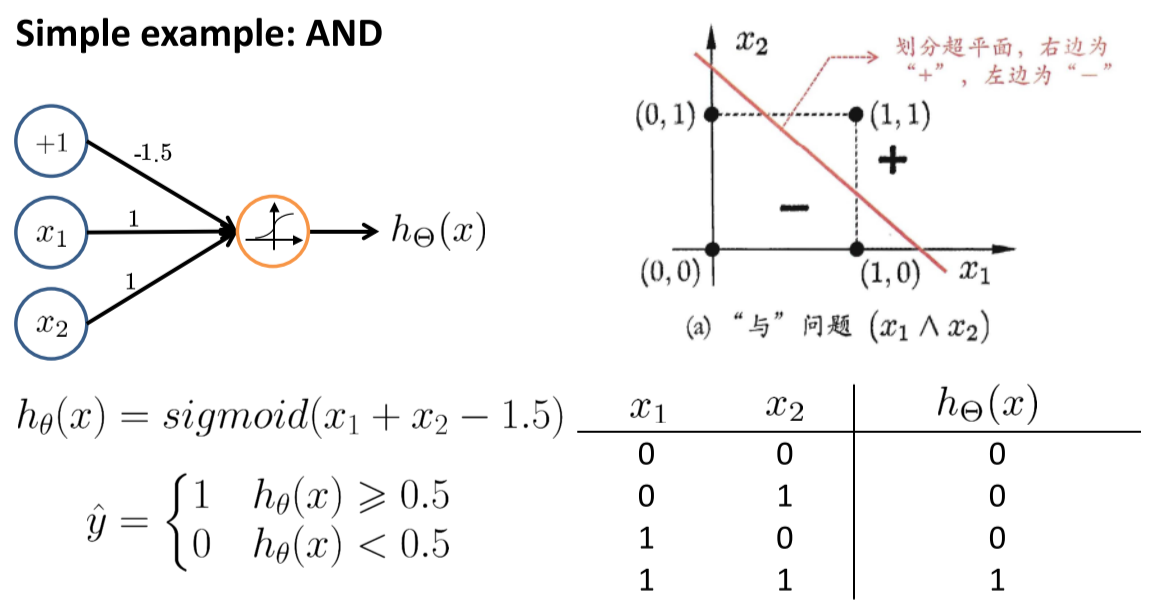

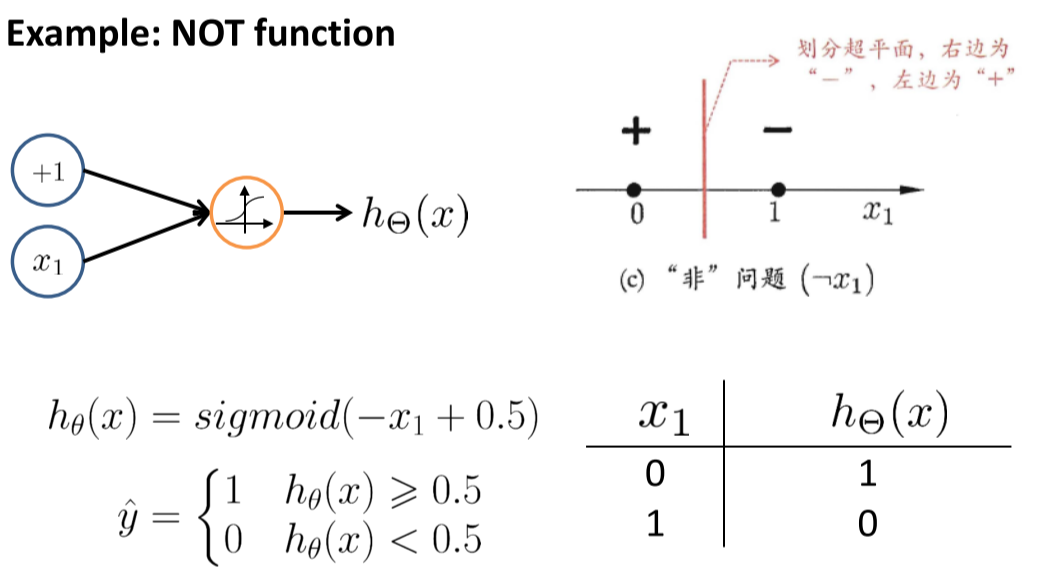
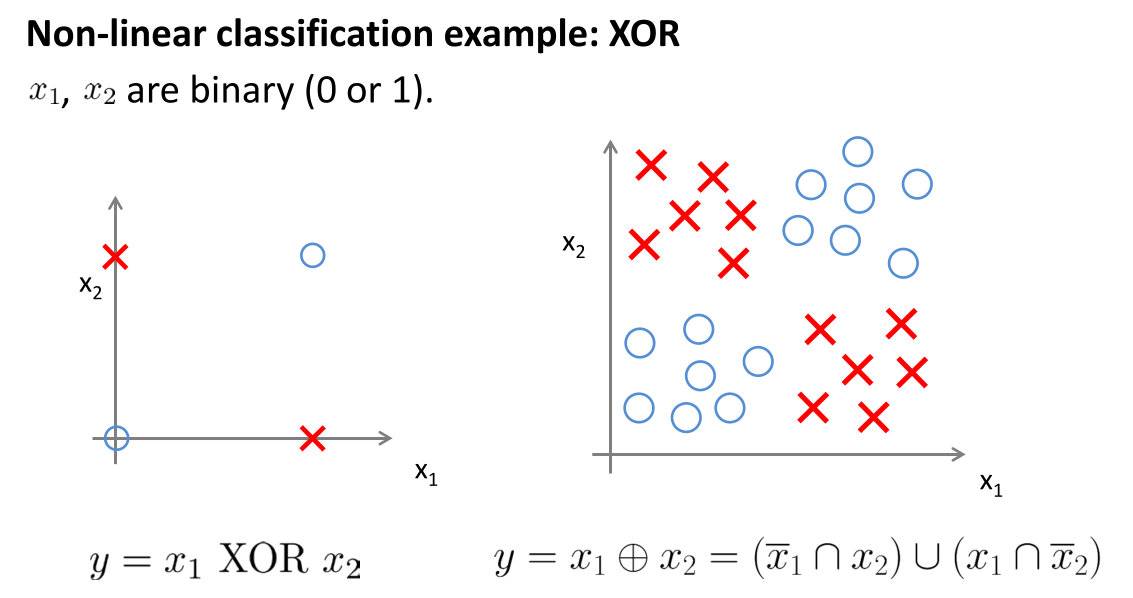
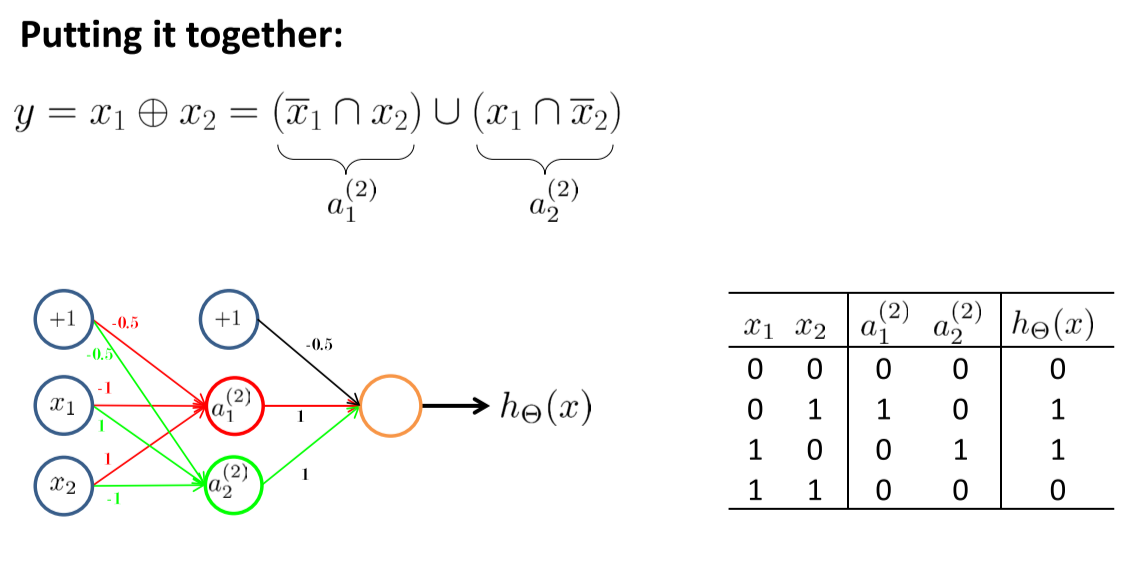
损失函数
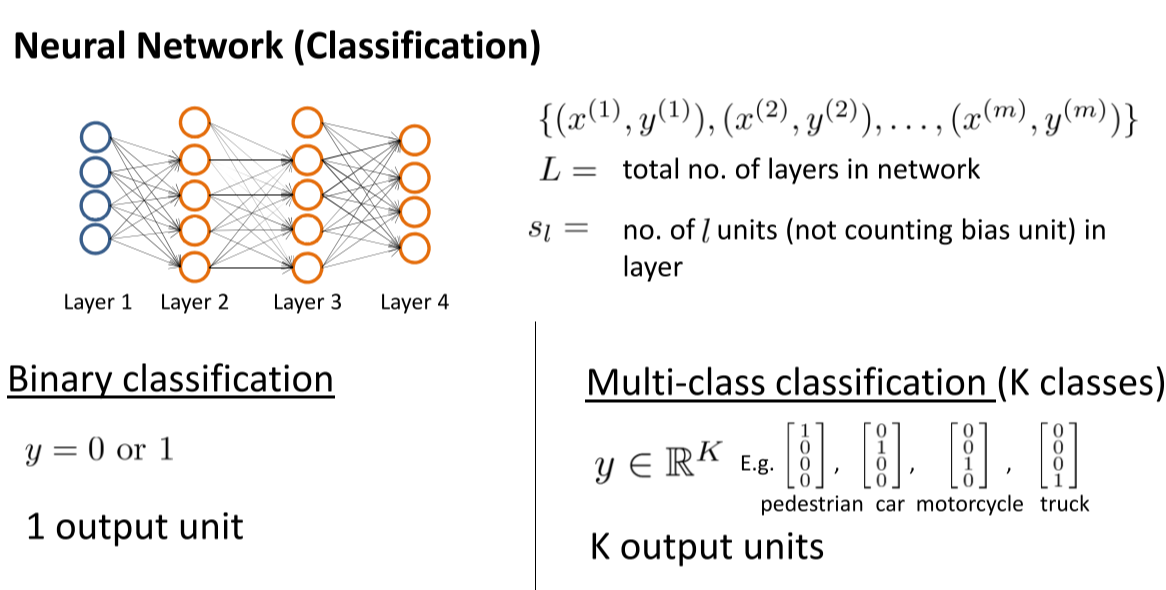
基于交叉熵的损失函数: $ J(\Theta)=-\frac{1}{m}\left[\sum_{i=1}^{m} \sum_{k=1}^{K} y_{k}^{(i)} \log \left(h_{\Theta}\left(x^{(i)}\right)\right){k}+\left(1-y{k}^{(i)}\right) \log \left(1-\left(h_{\Theta}\left(x^{(i)}\right)\right){k}\right)\right] +\frac{\lambda}{2 m} \sum{l=1}^{L-1} \sum_{i=1}^{s_{l}} \sum_{j=1}^{s_{l+1}}\left(\Theta_{j i}^{(l)}\right)^{2} $
基于平方误差的损失函数:$E_{k}=\frac{1}{2} \sum_{k=1}^{m} \sum_{j=1}^{l}\left(\hat{y}{j}^{k}-y{j}^{k}\right)^{2}$
优化
反向传播,懂得都懂,懒得写了
Deep Neural Network
了解一下就行了
Convolutional Neural Network
Long Short-Term Memory (LSTM) & RNN
Generative Adversarial Networks
SVM
Cost Function
- 线性可分问题最大化间隔策略
- 拉格朗日函数 $L(\mathbf{w}, b, \alpha)=\frac{1}{2}|\mathbf{w}|^{2}+\sum_{i=1}^{m} \alpha_{i}\left(1-y_{i}\left(\mathbf{w}^{T} \mathbf{x}_{i}+b\right)\right)$
- 经验风险:$\sum_{i=1}^{m} \alpha_{i}\left(1-y_{i}\left(\mathbf{w}^{T} \mathbf{x}{i}+b\right)\right)$ ,理想情况下,$y_i$ 和 $\mathbf{w}^{T} \mathbf{x}{i}+b$ 输出相同,损失为 $0$
-
结构风险:$\frac{1}{2}|\mathbf{w}|^{2}=\frac{1}{2} \sum_{j=1}^{n} \mathbf{w}^{2}$ 。两类样本的margin,点到直线距离为 $\frac{\left \mathbf{w}^{T} \mathbf{x}+b\right }{|\mathbf{w}|}$ ,所以,直线 $\mathbf{w}^{T} \mathbf{x}+b=1$ 到 $\mathbf{w}^{T} \mathbf{x}+b=0$ 距离为 $\frac{1}{|\mathbf{w}|}$
Prediction Model
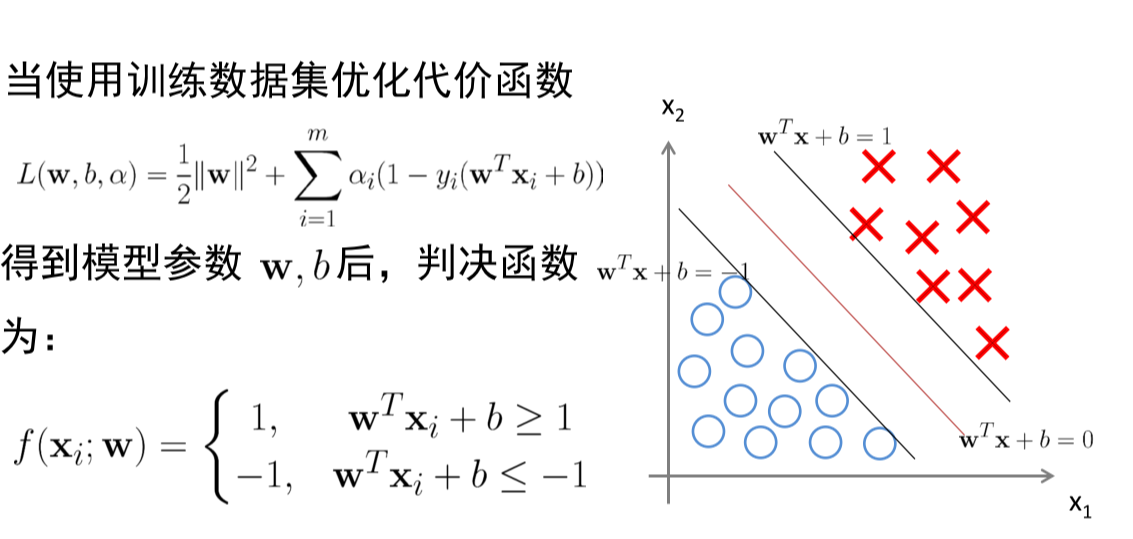
Optimize the Cost Function
看PPT,太多了
Kernel Technology
- 核函数是一个内积函数,$K(\mathbf{x}, \mathbf{y})=\langle\phi(\mathbf{x}), \phi(\mathbf{y})\rangle$
- 其中,$\phi$ 为 $X$ 到特征空间 $F$ 的一个映射
- 多项式核:$K(\mathbf{x}, \mathbf{y})=(\gamma\langle\mathbf{x}, \mathbf{y}\rangle+c)^{d}$
- 高斯核:$K(\mathbf{x}, \mathbf{y})=\exp \left(\frac{-|\mathbf{x}-\mathbf{y}|}{\sigma^{2}}\right)$
- Sigmoid 核:$K(\mathbf{x}, \mathbf{y})=\tanh (\gamma\langle\mathbf{x}, \mathbf{y}\rangle+c)$
决策函数写为:$f(x)=\sum_{i=1}^{m}\alpha_iy_iK(x,x_i)+b$
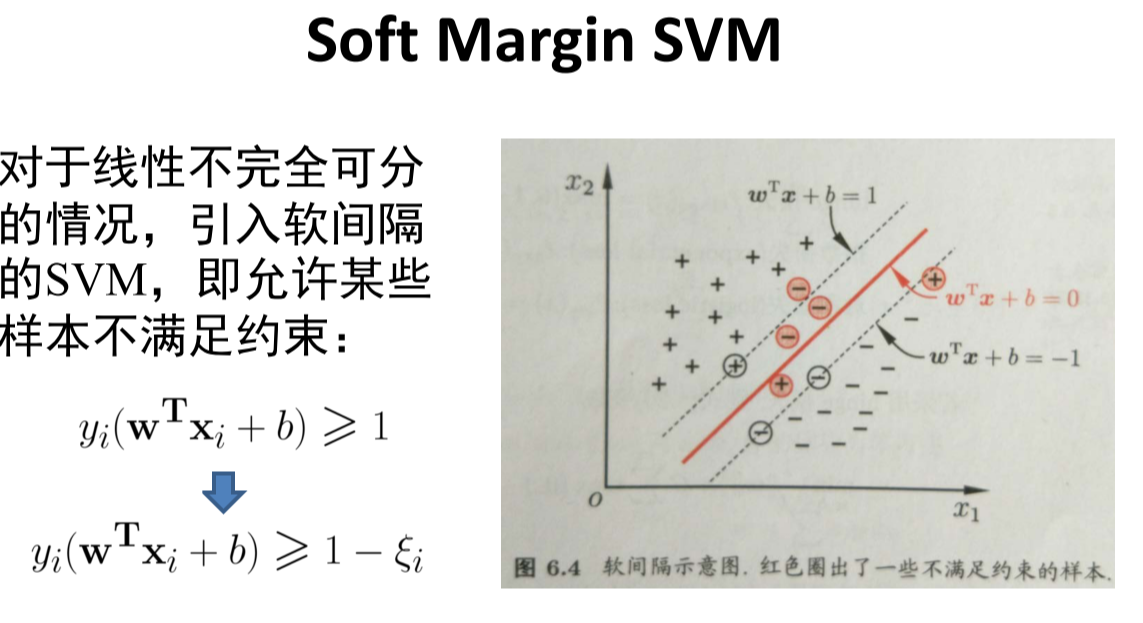
Soft Margin
数据并不完全是线性可分的,可能有不能满足约束的样本。允许分类器在一些样本上出错,引入软间隔。
机器学习评估
回顾
结果评估
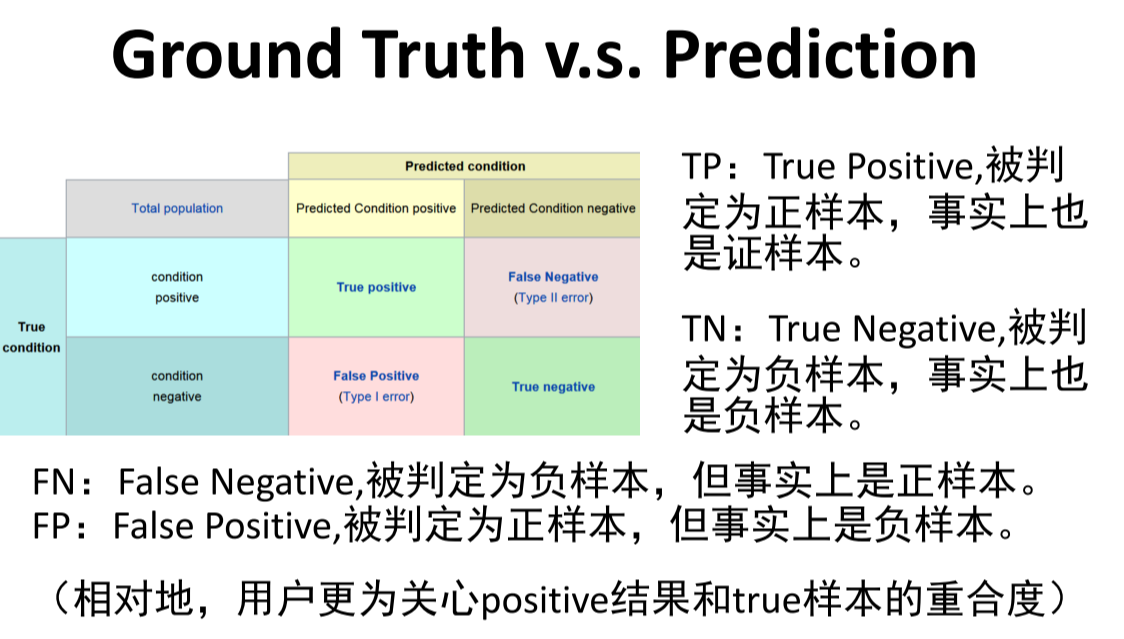
-
准确率
-
精确率(precision):$precision=\frac{TP}{TP+FP}$
-
召回率(recall):$recall=\frac{TP}{TP+FN}$
-
F-score:$F_1=2\frac{precision\times recall}{precision+recall}$
-
ROC:
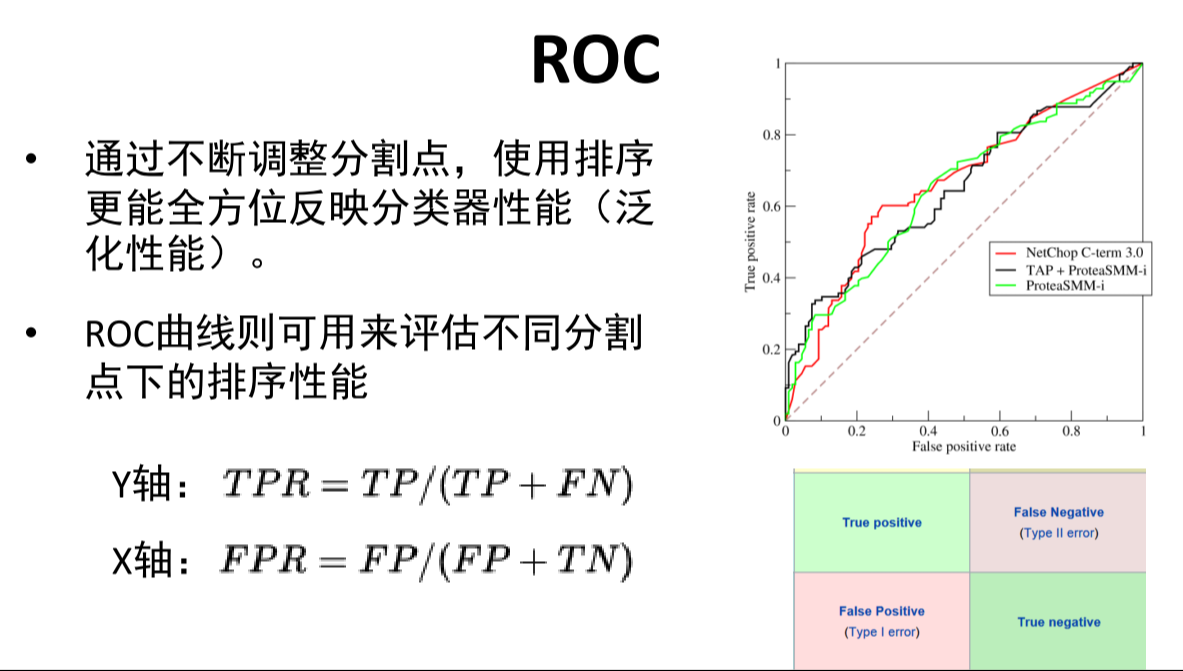
-
AUC:若随机抽取一个true样本和一个false样本,AUC表示分类器接受true样本高于接受false样本的概率。
计算:ROC积分面积
交叉验证
将整个训练数据分为n份,选择其中一份作为验证数据集,其余n-1作为训练集
模型评估
- 期望输出与真是标记之间的差别称为偏差(bias),$bias^2(x)=(f(x)-y)^2$
- 使用样本数相同的训练集产生的方差(variance):\frac{\part L(W,H)}{\part H_{kj}}=c[\sum_{i}W_{ik}V_{ij}-\sum_{i}(WH){ij}W{ik}]
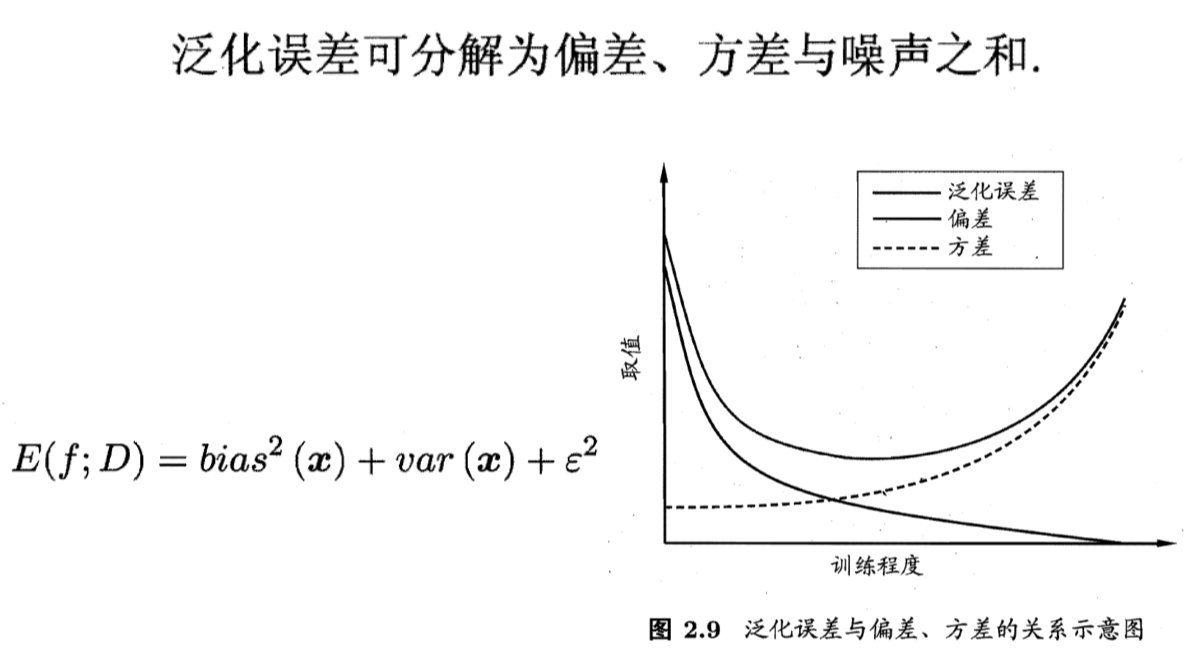
- 结构风险与经验风险:结构风险用来惩罚模型复杂度,例如正则化项(regularization)。经验风险用来最小化损失。
Bayes Classification
贝叶斯理论
-
贝叶斯公式:$P(A B)=\frac{P(B A)P(A)}{P(B)}$ -
全概率公式:$P(B)=\sum_{i=1}^{n}P(A_i)P(B A_i)$ -
贝叶斯定理
$P(c \boldsymbol x)=\frac{P(c, \boldsymbol x)}{P(\boldsymbol x)}=\frac{P(c)P(\boldsymbol x c)}{P(\boldsymbol x)}$ - $P(\boldsymbol x)$ 表示样本 $\boldsymbol x$ 在样本空间中出现的概率
-
$P(\boldsymbol x c)$ 表示样本 $\boldsymbol x$ 相对于类别标记 $c$ 的类条件概率,或称为似然 - $P(c)$ :$\mathcal{Y}$ 中各 $c \in \mathcal{Y}$ 的先验概率
朴素贝叶斯分类器
-
在估计 $P(\boldsymbol x c)$ 时很难估计 $\boldsymbol x$ 所有维联合发生的概率,原因在于很难用频率估计概率,因此,通过假设“各维度条件独立”,将联合概率变为各维度概率连乘 $P(c \mid \boldsymbol{x})=\frac{P(c) P(\boldsymbol{x} \mid c)}{P(\boldsymbol{x})}=\frac{P(c)}{P(\boldsymbol{x})} \prod_{i=1}^{d} P\left(x_{i} \mid c\right)$
-
由于对于给定 $\boldsymbol x$ 其 $P(\boldsymbol x)$ 对于所有 $c\in \mathcal{Y}$ 是一样的,因此判别函数简化为:
$h_{n b}(\boldsymbol{x})=\arg \max {c \in \mathcal{Y}} P(c) \prod{i=1}^{d} P\left(x_{i} \mid c\right)$
判别函数计算
-
类先验概率 $P(c) = \frac{ D_c }{D}$ -
若为离散属性的样本输入,类条件概率为:$P(x_i c)=\frac{ D_{c,x_i} }{ D_c }$ -
若为连续属性的输入,类条件概率为:$P(x_i c)=\frac{1}{\sqrt{2 \pi} \sigma_{c, i}} \exp \left(-\frac{\left(x_{i}-\mu_{c, i}\right)^{2}}{2 \sigma_{c, i}^{2}}\right)$ - 拉普拉斯修正:
-
$\hat{P}(c)=\frac{\left D_{c}\right +1}{ D +N}$ -
$\hat{P}\left(x_{i} \mid c\right)=\frac{\left D_{c, x_{i}}\right +1}{\left D_{c}\right +N_{i}}$
-
生成式模型
贝叶斯定理是生成式模型:需要对样本的分布进行建模再估计
| 判决式模型直接估计 $P(c | \boldsymbol x)$ |
极大似然估计(MLE)
学过概率论的都会,懂得都懂
贝叶斯信念网
-
使用有向无环图(DAG)来刻画属性之间的依赖关系,并使用条件概率表(CPT)来描述属性之间的联合概率分布
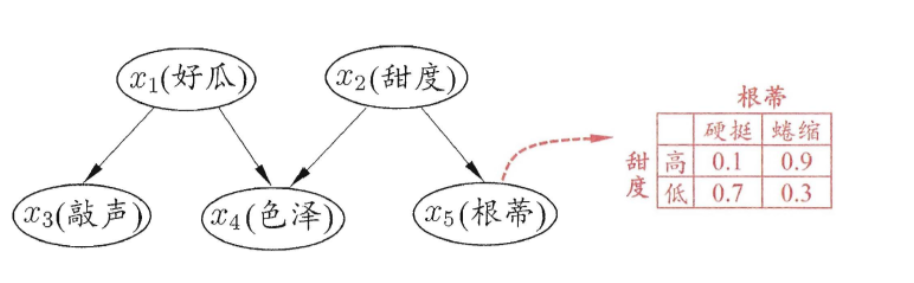
-
贝叶斯网结构有效地表达了属性见的条件独立性,给定父节点集,贝叶斯网假设每个属性与它的非后裔属性独立,于是 $B=<G,\Theta>$ 将属性 $x_1,x_2,…,x_d$ 的联合概率分布定义为:
$P_{B}\left(x_{1}, x_{2}, \ldots, x_{d}\right)=\prod_{i=1}^{d} P_{B}\left(x_{i} \mid \pi_{i}\right)=\prod_{i=1}^{d} \theta_{x_{i} \mid \pi_{i}}$
-
适用:
- 多维变量中联合概率估计时属性组合爆炸问题
- 样本稀疏导致概率估计值为0的问题
贝叶斯与信息检索语言模型
就是 N-gram 模型,自己查去吧,懂得都懂
EM 算法
这玩意不会考的,我说的!懂得都懂
Learning from Network
Examples: PageRank & SCI
- 网络检索
- SCI
- 基因网络
PageRank 随机游走算法
- 计算出转移概率矩阵
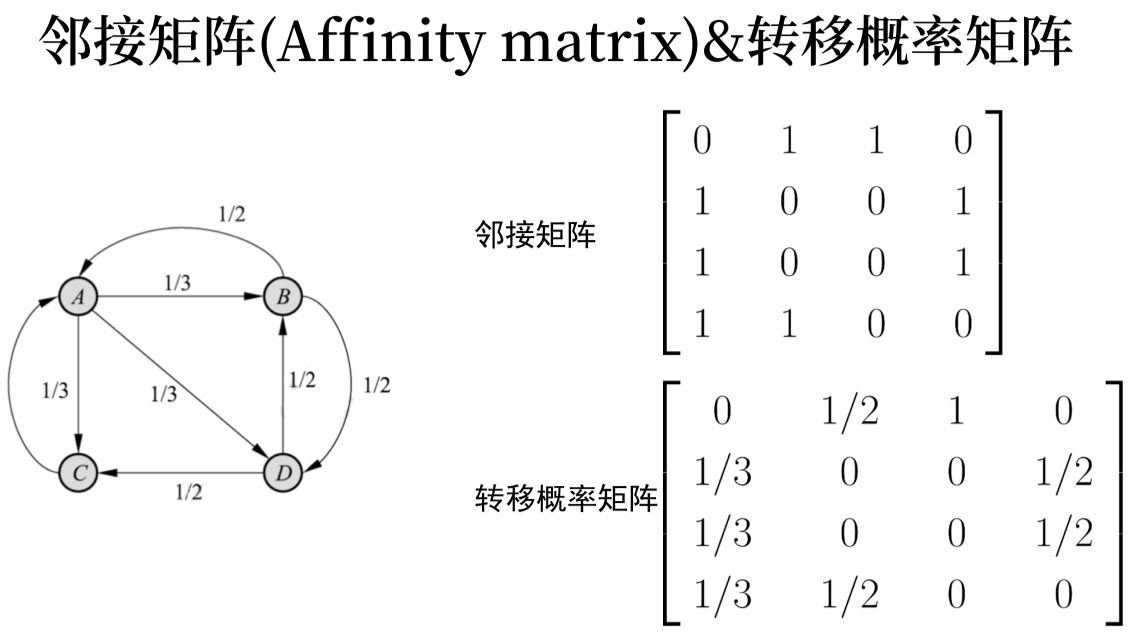


Different Representation of Relations
Cost Function of Random Walk with Restart
$\mathcal{Q}(F)=\frac{1}{2}\left(\sum_{i, j=1}^{n} W_{i j}\left|\frac{1}{\sqrt{D_{i i}}} F_{i}-\frac{1}{\sqrt{D_{j j}}} F_{j}\right|^{2}+\mu \sum_{i=1}^{n}\left|F_{i}-Y_{i}\right|^{2}\right)$
- 定义矩阵 $W$ ,$W_{i j}=\exp \left(-\left|x_{i}-x_{j}\right|^{2} / 2 \sigma^{2}\right)$
- 构建矩阵 $S$ ,$S=D^{-1 / 2} W D^{-1 / 2}$ 。其中,$D$ 是对角矩阵,对角线上元素为 $W$ 每行之和
-
迭代 $F(t+1)=\alpha S F(t)+(1-\alpha) Y$
- 游走足够远之后的极限值:
\(F(t)=(\alpha S)^{t-1} Y+(1-\alpha) \sum_{i=0}^{t-1}(\alpha S)^{i} Y
\\
\lim _{t \rightarrow \infty}(\alpha S)^{t-1}=0, \text { and } \lim _{t \rightarrow \infty} \sum_{i=0}(\alpha S)^{i}=(I-\alpha S)^{-1}
\\
F^{*}=\lim _{t \rightarrow \infty} F(t)=(1-\alpha)(I-\alpha S)^{-1} Y\)

How to Prioritize Heterogenenous Query
Ensemble Learning
集成学习
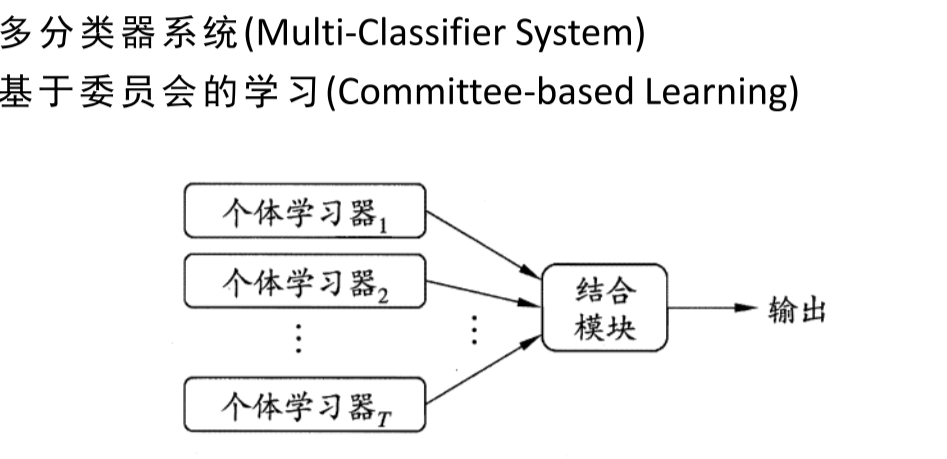
Boosting & AdaBoost PAC 可学习
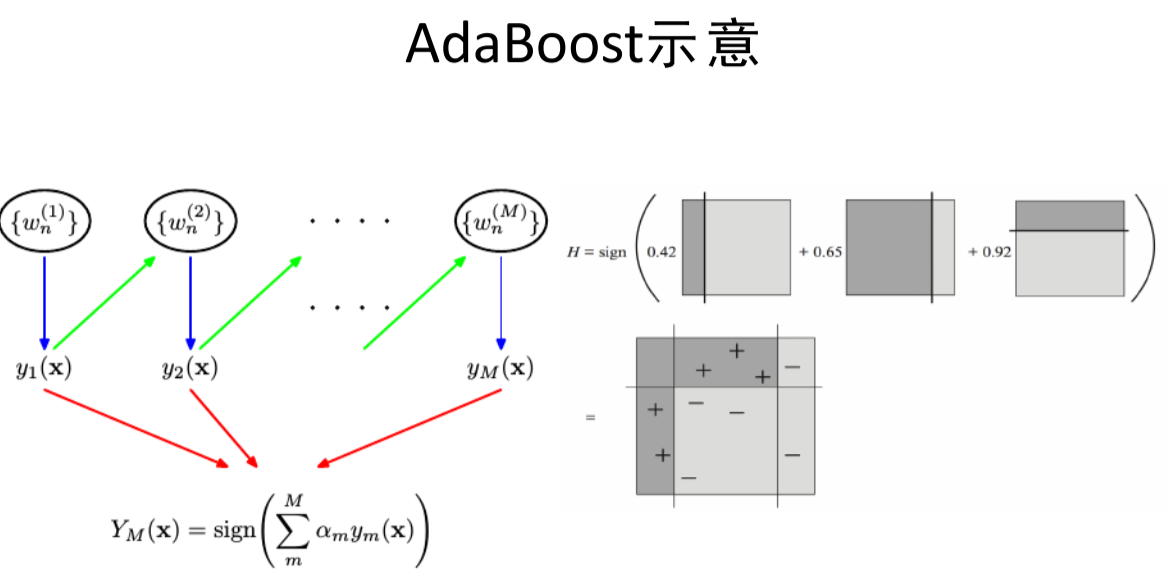
算法

Bagging、Bootstrap 抽样 随机森林
- Bagging:每次抽一个放回,操作m次,得到一个数据集,用不同的子数据集去训练然后集成
- 随机森林(Random Forest):决策树为基学习器构建Bagging集成分类器
Stacking
Clustering
聚类介绍
- 聚类目标:对数据进行聚合,使形成一些簇(类),用以了解数据的内在性质及规律
- 聚类原则:物以类聚
- 聚类结果:相似的聚为一类
-
地位:了解数据分布的工具
- 问题描述:输入 $D=\left{\boldsymbol{x}{1}, \boldsymbol{x}{2}, \ldots, \boldsymbol{x}{m}\right} \quad \boldsymbol{x}{i}=\left(x_{i 1} ; x_{i 2} ; \cdots ; x_{i n}\right)$ ,输出 $x \in C_{l}$
Performance Measure
- 簇内相似度(intra-cluster similarity)
- 簇间相似度(inter-cluster similarity)
- Jaccard 系数:$JC = \frac{a}{a+b+c}$
- FM 指数:$FMI=\sqrt{\frac{a}{a+b}\frac{a}{a+b}}$
- Rand 指数:$RI=\frac{2(a+d)}{m(m-1)}$
-
簇内样本平均距离:$\operatorname{avg}(C)=\frac{2}{ C ( C -1)} \sum_{1 \leqslant i<j \leqslant C } \operatorname{dist}\left(\boldsymbol{x}{i}, \boldsymbol{x}{j}\right)$ -
簇内样本最远距离:$\operatorname{diam}(C)=\max _{1 \leqslant i<j \leqslant C } \operatorname{dist}\left(\boldsymbol{x}{i}, \boldsymbol{x}{j}\right)$ - 簇间距离:$d_{\min }\left(C_{i}, C_{j}\right)=\min {\boldsymbol{x}{i} \in C_{i}, \boldsymbol{x}{j} \in C{j}} \operatorname{dist}\left(\boldsymbol{x}{i}, \boldsymbol{x}{j}\right)$
-
簇间距离:$d_{\text {cen }}\left(C_{i}, C_{j}\right)=\operatorname{dist}\left(\boldsymbol{\mu}{i}, \boldsymbol{\mu}{j}\right)$
- DBI 指数:$\mathrm{DBI}=\frac{1}{k} \sum_{i=1}^{k} \max {j \neq i}\left(\frac{\operatorname{avg}\left(C{i}\right)+\operatorname{avg}\left(C_{j}\right)}{d_{\operatorname{cen}}\left(\boldsymbol{\mu}{i}, \boldsymbol{\mu}{j}\right)}\right)$
- Dunn 指数:$\mathrm{DI}=\min {1 \leqslant i \leqslant k}\left{\min _{j \neq i}\left(\frac{d{\min }\left(C_{i}, C_{j}\right)}{\max {1 \leqslant l \leqslant k} \operatorname{diam}\left(C{l}\right)}\right)\right}$
Kmeans 算法
-
给定样本集 $D=\left{\boldsymbol{x}{1}, \boldsymbol{x}{2}, \ldots, \boldsymbol{x}{m}\right}$ ,Kmeans算法针对所有簇 $\mathcal{C}={C_1,C_2,…,C_k}$ 最小化平方误差 $E=\sum{i=1}^{k}\sum_{\boldsymbol x\in C_i} \boldsymbol x-\boldsymbol \mu_i _2^2$

其他聚类算法
- 基于密度聚类(density-based clustering):假设聚类结构能够通过样本分布的紧密程度确定。算法:DBSCAN(Density-Based Spatial Clustering of Applications with Noise)
- 层次聚类(hierarchical clustering):试图在不同层次对数据集进行划分,从而形成树形的聚类结构。算法:AGNES(AGglomerative NESting)
Dimension Reduction
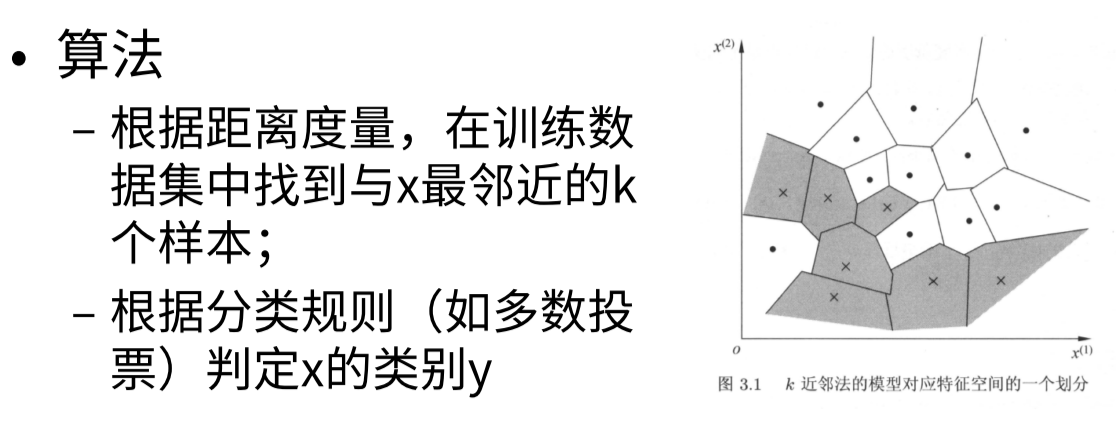
K-Nearest Neighbor Classification
Principle Component Analysis


- PAC 使用:
- 数据压缩,维度约减
- 不适合防止过拟合
Non-negative Matrix Factorization
-
特征压缩、软聚类
-
应用:图像特征抽取、文本语义模型、基因数据分析
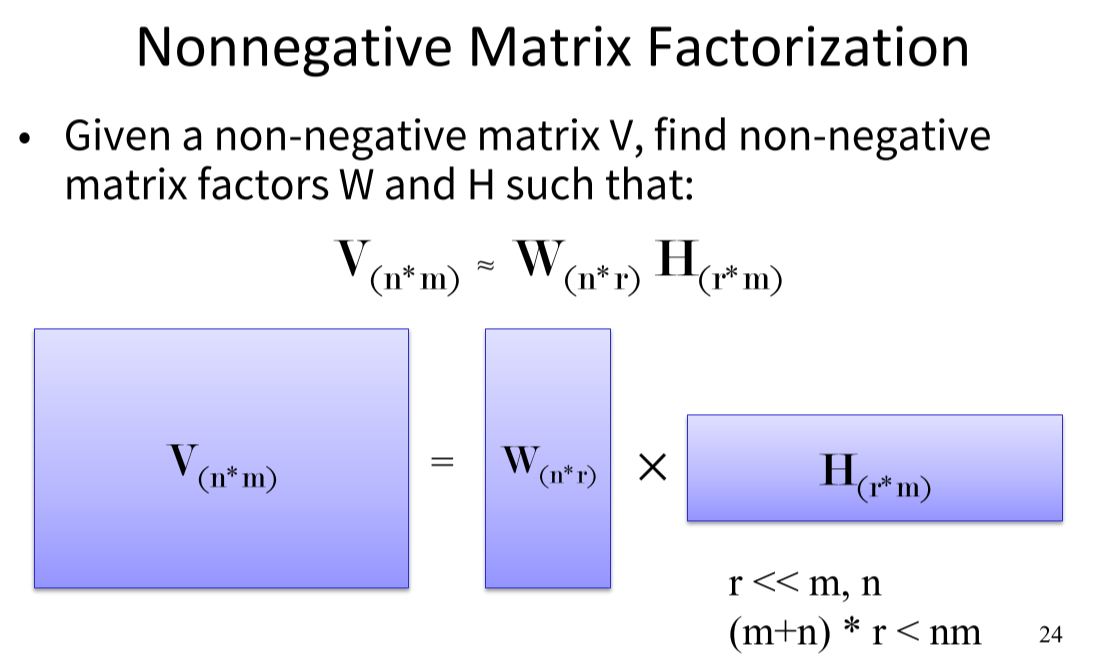
损失
分解前后误差:$E=V-WH$
| 损失 $min_{WH} | V-WH | $ |
假设噪声 $E$ 符合高斯分布
| $p(E | W,h)=\frac{1}{\sqrt{2\pi}\sigma_{ij}}exp(-\frac{E_{ij}^2}{2\sigma_{ij}^2})$ |
构造似然函数: \(\{W,H\}=argmax_{W,H} p(V|W,H)=argmin_{W, H}\{-logp(V|W,H)\} \\ L(W,H)=\frac{1}{2\sigma_{ij}^2}\sum_{ij}(V_{ij}-(WH)_{ij})^2+\sum_{ij}log(\sqrt{2\pi}\sigma_{ij})\)
优化
\[L(W,H)=\frac{1}{2\sigma_{ij}^2}\sum_{ij}(V_{ij}-(WH)_{ij})^2+\sum_{ij}log(\sqrt{2\pi}\sigma_{ij}) \\ \begin{aligned} \frac{\part L(W,H)}{\part W_{ik}}&=c[\sum_jH_{kj}(V_{ij}-(WH)_{ij})] \\ &=c[\sum_jV_{ij}H_{kj}-\sum_j(WH)_{ij}H_{kj}] \\ &=c[(VH^T)_{ik}-(WHH^T)_{ik}] \end{aligned} \\ \begin{aligned} \frac{\part L(W,H)}{\part H_{kj}}&=c[\sum_{i}W_{ik}V_{ij}-\sum_{i}(WH)_{ij}W_{ik}] \\ &=c[(W^TV)_{kj}-(W^TWH)_{kj}] \end{aligned}\]Theory of Machine Learning
偏差、方差理论
- 偏差:期望输出与真实标记的差别称为偏差。$bias^2(x)=(f(x)-y)^2$
- 方差:使用样本数相同的不同训练集产生的方差。$\frac{\part L(W,H)}{\part H_{kj}}=c[\sum_{i}W_{ik}V_{ij}-\sum_{i}(WH){ij}W{ik}]$

过拟合
- 低偏差意味着经验风险最小化
- 低偏差意味着结构风险最小化
正则化
为了避免过拟合,使用正则化项来惩罚结构风险
结构风险最小化(VC 维、SVM、模型惩罚、正则化)

从统计角度看机器学习
统计学习的目标是找到一个映射,使得的期望最小。所以,统计学习本质上来说是一个最优化问题。

PAC 学习理论
- 概率近似正确(Probably Approximately Correct,PAC)
- PAC 辨识,学习算法 L 能够从假设空间对中辨识概念类 C
- PAC 可学习:从假设空间 H 中 PAC 辨识出概念类 C,则称概念类 C 对假设空间 H 而言是 PAC 可学习的。