并行复习重点

绪论

推动并行计算的原因

1. 处理器能力：晶体管集成密度在提高，但是时钟频率提高速度急剧放缓。频率提升已经不是处理器发展的主角。
2. 功耗/散热的限制，单个处理器核心如果要提升频率，功耗会更高，难以散热。
3. 性能上升放缓

了解并行计算应用

科学仿真：进行理论或纸面设计；进行实验或构建系统

• 科学仿真的一般方法：
  1. 将物理或概念空间化为离散化网格
  2. 在网格上进行局部计算
  3. 网格局部结果交互
  4. 重复若干时间步
  5. 可能对结果进行其他计算

• 科学仿真的例子：

  1. 全球气候建模：

• 需要构造一个函数 $f(维度, 精度, 海拔, 时间) -> 温度, 压力, 湿度, 风力$。

• 方法：离散化大气层，将大气层网格化，并设计算法，对于给定的$t$时刻，预测$t+\delta t$时刻的天气。

• 应用：预测重要气候趋势，例如厄尔尼诺现象。设定空气排放标准

• 为什么需要并行计算：大气层网格化后，格点数目巨大。如果采用串行计算，耗时极大。
  1. 海洋建模
  2. 星系演化：每个时间步计算N个星体之间的引力。计算出每个星体的运动趋势，若干时间步内星系的运动规律。
  3. 生物信息学
  4. 强子对撞机实验
  5. 天文学：天文望远镜采集的极大量数据的处理。
  6. 医学：X光、CT的在线存储、数据分析
  7. 商业应用
  8. 人工智能

超算机

1. 神威太湖之光（Sunway TaihuLight）
2. 顶点（Summit）

E级超算：

1. 天河三号：2018年8月部署启用
2. 中科曙光（2020年完成）
3. 美国极光（Aurora）
4. 日本后京（Post-K）

并行计算面临的挑战

• 并行程序的复杂性

  1. 足够的并发度
  2. 并发粒度（独立计算的任务大小）
  3. 负载均衡（处理器之间的工作量相近）
  4. 协调和同步

• 数据移动代价很高

  移动单位量数据的代价很高。

• 能耗挑战

• 伸缩性挑战

  1. 相同的程序在新一代硬件架构下仍能高效运行。
  2. 在更大规模（更多核心）的硬件平台下仍能高效运行

• 软件面临的挑战

  1. 硬件技术发展飞速，软件生态停滞
  2. 关注现有软件难以处理的硬件发展趋势：众核、异构、每CPU内存
  3. 新软件技术不够成熟：UPC、Cilk、CUDA
  4. 现有代码还未准备好硬件架构的改变

并行硬件和并行软件

Cache 相关工作原理

Cache 概念

A collection of memory locations that can be accessed in less time than some other memory locations.

相比其他内存，Cache是一块可以被更快访问的内存地址。

A CPU cache is typically located on the same chip, or one that can be accessed much faster than ordinary memory.

CPU缓存通常位于同一芯片上，或者比普通内存访问速度更快。

局部性原理

正在运行的程序，会访问空间上相邻的指令或者是时间上相邻的

缓存可以根据以上规则进行设计

多级缓存

一个 CPU 大多有多个缓存，L1、L2、L3

缓存命中

当命中后写数据时，需要决定如何写回

当 CPU 更改了 Cache 的数据，如何更新到主存？

• 写直达法（Write-through）：一旦更改，立刻更新
• 写回法（Write-back）：CPU 更改了 Cache 中的数据后，标记为脏（dirty）数据项。执行完毕后，统一将脏数据写回。

缓存未命中

需要做缓存映射，但是不重要，不用掌握

1. 全相联（Full associative）
2. 直接映射（Direct mapped）
3. N 路相连（N-way set associastive）

并行和多线程概念

• 进程：一个正在执行的计算机程序实例
• 多任务：在单核的机器上并发的执行多个程序。时分复用。
• 线程：线程由进程包含，线程支持程序员将程序分为多个独立的任务。

Flynn 分类法

只关心 SIMD 和 MIMD

SIMD

• 概念：将数据分配给多个处理单元，在多个数据项上执行相同的操作，被称为数据并行
• SMID 缺点
  • 所有计算单元必须执行相同指令，或者有单元需要空转
  • 计算单元必须同步
  • 计算单元没有指令存储功能
  • 只适合数据量大的并行问题
• 能对数组、数据向量进行操作

MIMD :star:

• 概念：支持多个同步指令流在多个数据流上操作。由一些完全独立的处理单元或核心组成，每个都有自己的控制单元和 ALU。每个处理器能够按照自己的需求进行处理，没有统一的时钟。

共享内存系统

一组自治的处理器，通过互联网络与内存链接。

• 每个处理器可以访问每一块内存

• 处理器通过分享数据来进行隐式通信。

• 一个多核处理器或者多个多核处理器组成，通过互联网络来链接。

• 一致内存访问系统，处理器间无链接

  

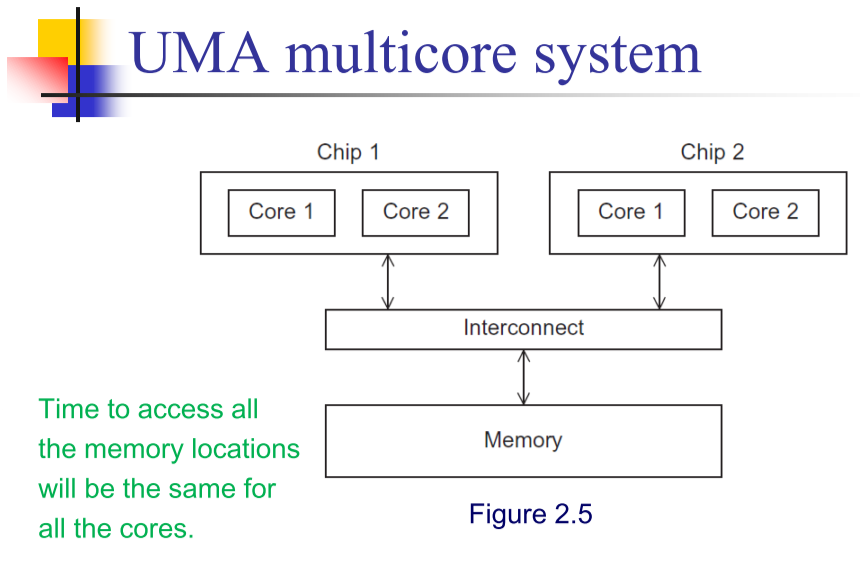
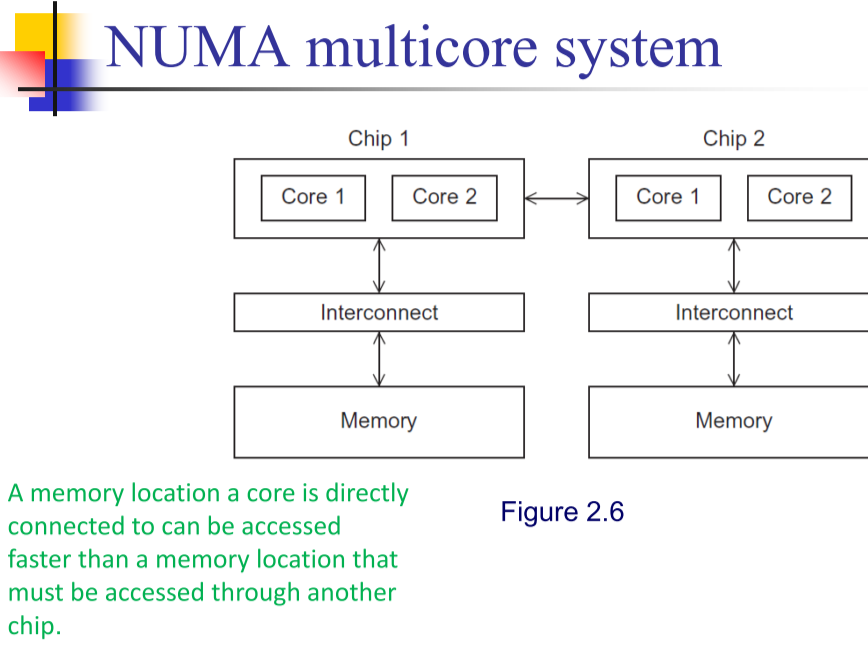
• 非一致内存访问系统，处理器之间进行通信（仍然是共享内存，比较少见）。

  

分布内存系统

• 集群，多态机器相连搭建成集群

  

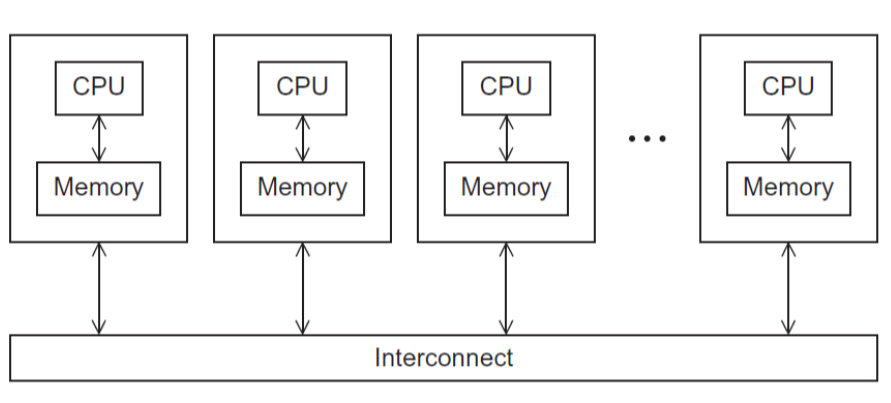
互联网络

共享内存互联网络

• 总线连接，只能有一对设备通信，多个设备会竞争总线

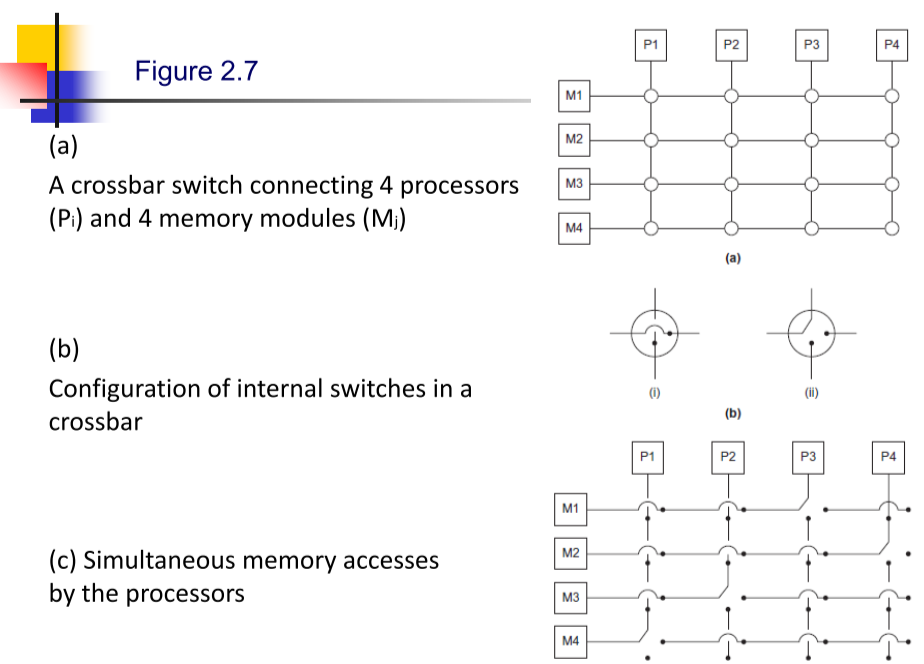
• 交换器控制，交叉开关矩阵。优点在于，不同 CPU 可以同时访问同一个内存模块。但是更贵，灵活性差。

  

  等分宽度

• 

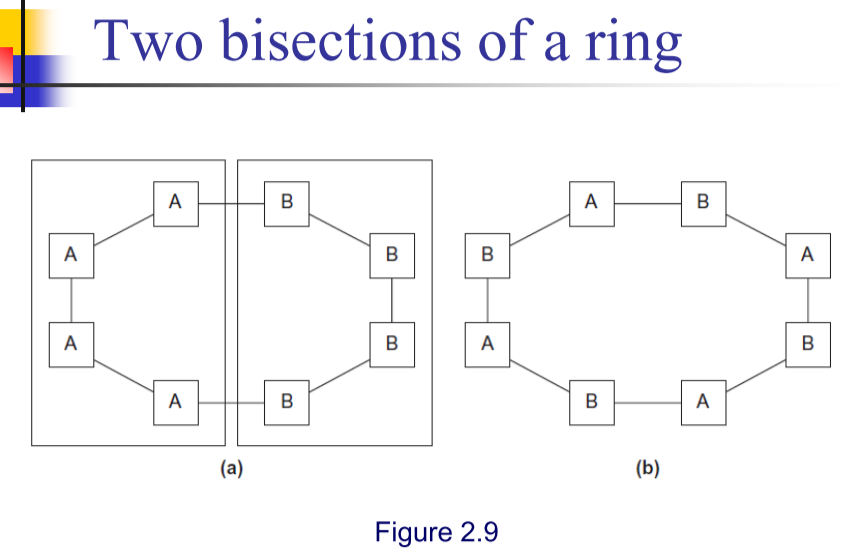
• 定义：同时通信的链路数目，衡量网络连接性的标准。等分成两份，看看有多少组节点能够相互通信（基于最坏情况评估）。环状的为 $2$ 。

等分带宽

来表示网络交换的速度，$宽度\times 单链路带宽$

分布式

• 直接互联：每一个交换器，直接与处理器、内存对链接。

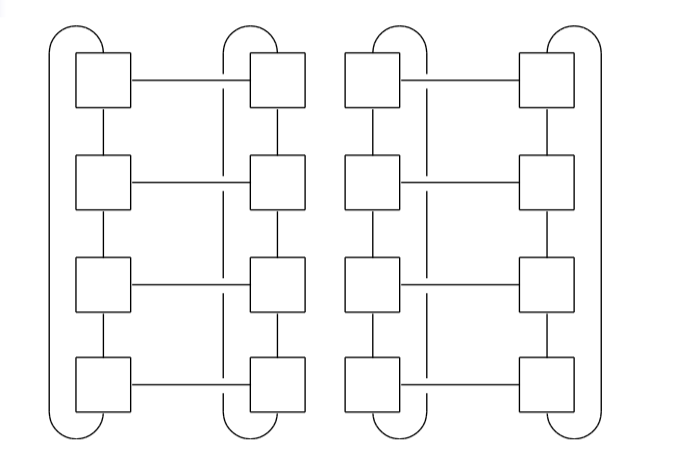
  • 环状、二维环面

    

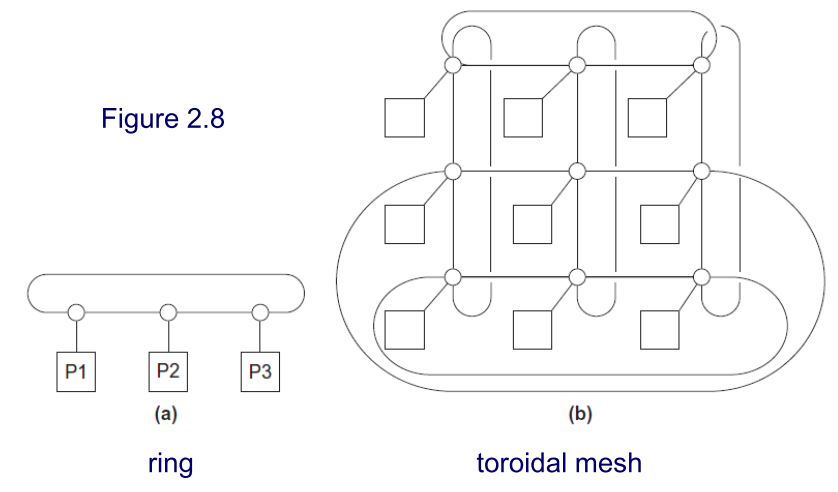
  • 二维环面网络结构，带宽为 $2\sqrt p$ ，其中 $p$ 为处理器数目。

    

    

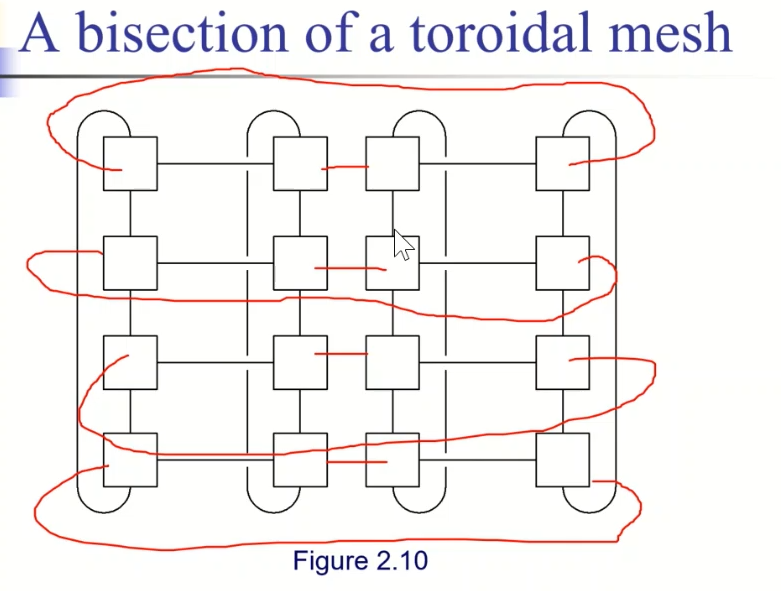
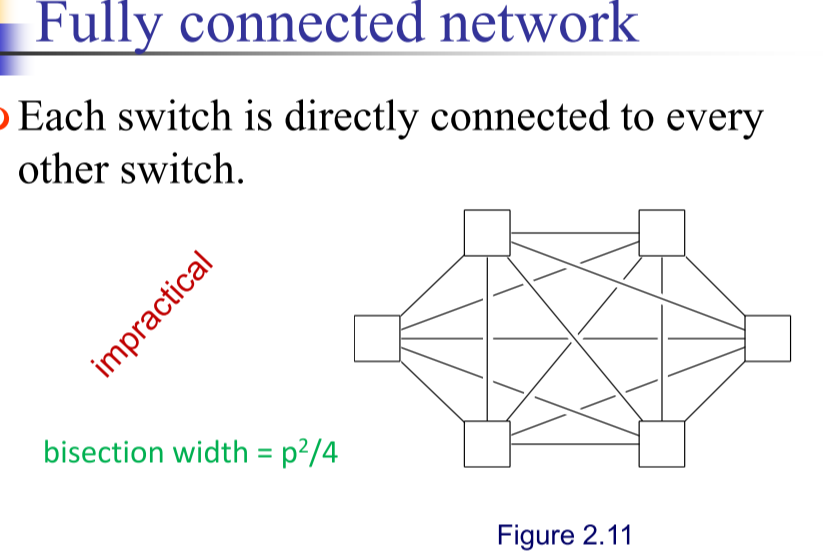
  • 全连接网络，宽度 $\frac{p^2}{4}$。现实中不实际，交换器造价高。

    

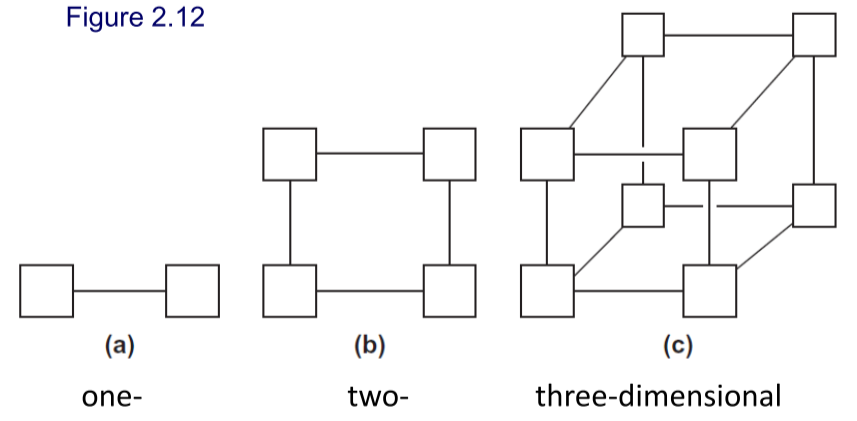
  • $d$ 维超立方，节点数为 $2^d$ ，等分宽度为 $\frac{p}{2}$ 。

    

• 间接互联（了解）

  • Crossbar
  • Omega network

并行算法设计

任务分解

• 要考虑负载均衡的问题
• 使得通信量尽量少

任务并行

将求解的问题的计算分解为任务，分配给多个核心

数据并行

将求解问题的数据划分给多个核心，然后每个核心对不同数据进行相似计算

数据依赖

循环步之间的运算存在依赖。

数据依赖（data dependence）就是两个内存操作的序，为了保证结果的正确性，必须保持这个序

• 原子性：一组操作要么全部执行，要么全部不执行，则称之为原子性的。
• 互斥：任何时刻都只有一个线程在执行。

竞争条件

执行结果依赖于两个或更多事件的时许，则存在竞争条件（race condition）

同步

在时间上强制使各进程/线程在某一点必须相互等待，确保各进程/线程的正常顺序和对共享可写数据的正确访问。

并行算法分析

• 运行时间：串行算法运行时间 $T_S$ ，并行算法运行时间 $T_P$ 。
• 并行算法额外总开销：$T_o=pT_P-T_S$

加速比

$S = \frac{T_S}{T_P}$

• $n$ 个数相加，使用 $n$ 个进程，加速比为 $\Theta(n/logn)$
• 串行冒泡排序算法用时150s，串行快排30s，并行冒泡40s，$S=30/40=0.75$，用快排时间算。
• 一般 $S<=p$
• 若 $S = p$，该并行算法具有线性加速比。
• 若 $S>p$，超线性加速比
  • Cache 引起的超线性加速比
  • 搜索分解导致超线性

效率

度量有效计算时间。

$E=S/p=T_S/(p\times T_P)$

理想情况下，$E=1$，正常情况 $0<E<1$ 。

可扩展性

若某并行程序核数（线程数/进程数）固定，并且输入规模也是固定的，其效率值为E。现增加程序核数（线程数/进程数），如果在输入规模也以相应增长率增加的情况下，该程序的效率一直是E（不降），则称 该程序是可扩展的。

• 强可扩展：我们希望保持问题规模不变时，效率不随着线程数的增大而降低，则称程序是可扩展的。
• 弱可扩展：问题规模以一定速率增大，效率不随着线程数的增大而降低，则认为程序是可扩展的。

阿姆达尔定律

除非一个串行程序的执行几乎全部都并行化，否则不论多少可以利用的核，通过并行化产生的加速比都会是受限的。

$S=1/(1-a+a/p)$

• $a$ 为串行程序中可以被完美并行化的比例
• $T_S=1$
• $T_P=T_{可并行}+T_{不可并行}=1-a+a/p$

SIMD 编程

SIMD编程的问题

打包解包开销

• 打包：打包源运算对象，拷贝到连续内存区域
• 解包：解包目的运算对象，拷贝回内存

对齐开销

• 对齐的内存访问：地址总是向量长度的倍数（16字节）
• 未对齐的内存访问
  • 地址不是16字节的整数倍
  • 静态对齐：对未对齐的读操作，做两次相邻的对齐读操作，然后进行合并
  • 有时候硬件帮你做，但是仍然会产生多次内存开销
  • 动态对齐：合并点在运行时计算

控制流开销

如果执行过程中的控制流发生了变化怎么办？

• 当前的商用编译器不太可能支持控制流优化
• 在存在控制流问题时，SIMD不是一个好的模型
• 一些情况下可以加速

SIMD 编程

SSE 关键字

• 类型

  __m128: float
  __m128d: double
  __m128i: integer
  

• 数据移动和初始化

  _mm_load_ps
  _mm_loadu_ps
  _mm_load_pd
  _mm_loadu_pd
    
  _mm_store_ps
  _mm_setzero_ps
  

• 命名规则

  • 第一部分是前缀_mm
  • 第二部部分是指令说明，例如_add，_mul，_load。有些可能有修饰符，例如loadu将16位未对齐的操作数加载到寄存器。
  • 第三部分为操作的对象名及数据类型，_ps packed 操作所所有的单精度浮点数。_pd 操作所有的双精度浮点数。_pixx 表示操作不同长度的有符号整数，使用64位寄存器。_epixx 表示操作不同长度有符号整数，使用128位寄存器。

DEMO

void sse_mul(int n, float a[][maxN], float b[][maxN], float c[][maxN]){
	__m128 t1, t2, sum;
    for (int i = 0; i < n; ++i)
        for (int j = 0; j < i; ++j)
            swap(b[i][j], b[j][i]);
    for (int i = 0; i < n; ++i) { 
        for (int j = 0; j < n; ++j) {
            c[i][j] = 0.0;
            sum = _mm_setzero_ps();
            for (int k = n - 4; k >= 0; k -= 4) {
				// sum every 4 elements
                t1 = _mm_loadu_ps(a[i] + k);
                t2 = _mm_loadu_ps(b[j] + k);
                t1 = _mm_mul_ps(t1, t2);
                sum = _mm_add_ps(sum, t1);
			}
			sum = _mm_hadd_ps(sum, sum);
            sum = _mm_hadd_ps(sum, sum);
			_mm_store_ss(c[i] + j, sum);
            for (int k = (n % 4) - 1; k >= 0; k--) {
                c[i][j] += a[i][k] * b[j][k];
            }
        }
    }
    for (int i = 0; i < n; i++) 
        for (int j = 0; j < i; j++)
            swap(b[i][j], b[j][i]);
}

void sse_tile(int n, float a[][maxN], float b[][maxN], float c[][maxN]) {
	__m128 t1, t2, sum;
    float t;
	for (int i = 0; i < n; ++i)
        for (int j = 0; j < i; ++j)
            swap(b[i][j], b[j][i]);
    for (int r = 0; r < n / T; ++r)
        for (int q = 0; q < n / T; ++q) {
            
            for (int i = 0; i < T; ++i)
                for (int j = 0; j < T; ++j)
                    c[r * T + i][q * T + j] = 0.0;
            
            for (int p = 0; p < n / T; ++p) {
                
                for (int i = 0; i < T; ++i)
                    for (int j = 0; j < T; ++j) {
                        sum = _mm_setzero_ps();
                        for (int k = 0; k < T; k += 4) {
                            t1 = _mm_loadu_ps(a[r * T + i] + p * T + k);
                            t2 = _mm_loadu_ps(b[q * T + j] + p * T + k);
                            t1 = _mm_mul_ps(t1, t2);
                            sum = _mm_add_ps(sum, t1);
                        }
                        
                        sum = _mm_hadd_ps(sum, sum);
                        sum = _mm_hadd_ps(sum, sum);
                        _mm_store_ss(&t, sum);
                        c[r * T + i][q * T + j] += t;
                    }
            }
        }
    for (int i = 0; i < n; ++i)
        for (int j = 0; j < i; ++j)
            swap(b[i][j], b[j][i]);
}

Pthread 编程

并行程序设计的复杂性

• 足够的并发度（Amdahl定律）
• 并发粒度
• 局部性
• 负载均衡
• 协调和同步

Ptread 一些基础API

int pthread_create(pthread_t*, const pthread_attr_t*, void* (*)(void*), void*);
int pthread_join(pthread_t *, void** value_ptr);

errcode = pthread_create(&thread_id, &thread_attribute, &thread_fun, &fun_arg);

• thread_id 线程指针
• thread_attribute 各种属性，通常用空指针表示标准属性
• thread_fun 新线程要运行的函数
• fun_arg 传递给函数的参数
• errcode 错误代码

同步相关概念

• 同步：在时间上强制使各执行进程/线程在某一点必须相互等待，确保各进程/线程的正常顺序和对共享可写数据的正常访问。
• 原子性：一组操作要么全部执行要么全部不执行，则称为原子的。
• 临界区：是一个更新共享资源的代码段，一次只能允许一个线程执行该代码段。
• 竞争条件：多个线程/进程尝试更新同一个共享资源时，结果可能是无法预测的，则存在竞争条件。
• 数据依赖：就是两个内存操作的序，为了保证结果的正确性，必须保持这个序。

忙等待

void *pi_busywaiting(void *parm) {
    threadParm_t *p = (threadParm_t *) parm;
    int r = p->threadId;
    int n = p->n;
    int my_n = n/THREAD_NUM;
    int my_first = my_n*r; 
    int my_last = my_first + my_n;
    double my_sum = 0.0;
    if (my_first % 2 == 0)
        factor = 1.0;
    else factor = -1.0;
    for (int i = my_first; i < my_last; i++, factor = -factor) {
        my_sum += factor / (2 * i + 1);
    }
    while (flag != r)
        Sleep(0);
    sum += my_sum;
    flag++;
    pthread_exit(nullptr);
}

互斥量

void *pi_mutex(void *parm) {
    threadParm_t *p = (threadParm_t *) parm;
    int r = p->threadId;
    int n = p->n;
    int my_n = n/THREAD_NUM;
    int my_first = my_n*r;
    int my_last = my_first + my_n;
    double my_sum = 0.0;
    if (my_first % 2 == 0)
        factor = 1.0;
    else factor = -1.0;
    for (int i = my_first; i < my_last; i++, factor = -factor) {
        my_sum += factor/(2*i+1);
    }
    pthread_mutex_lock(&mutex); sum += my_sum;
    pthread_mutex_unlock(&mutex);
    pthread_exit(nullptr);
}

信号量

// 初始化，pshared为0，进程内共享，非0进程间共享。value为初始值
int sem_init(sem_t* sem, int pshared, unsigned value);
// 减一，若为0阻塞
int sem_wait(sem_t* sem);
// 加一，若原来为0，则可能唤醒阻塞线程
int sem_post(sem_t* sem);
// 释放
int sem_destory(sem_t* sem);

typedef struct {
    int threadId;
} threadParm_t;
sem_t sem_parent;
sem_t sem_children;
void *threadFunc(void *parm) {
    threadParm_t *p = (threadParm_t *) parm;
    fprintf(stdout, "I am the child thread %d.\n", p->threadId);
    sem_post(&sem_parent);
    sem_wait(&sem_children);
    fprintf(stdout, "Thread %d is going to exit.\n", p->threadId);
    pthread_exit(NULL);
}
int main(int argc, char *argv[]) {
	sem_init(&sem_parent, 0, 0);
    sem_init(&sem_children, 0, 0); 
	pthread_t thread[NUM_THREADS];
	threadParm_t threadParm[NUM_THREADS];
	int i;
    for (i=0; i<NUM_THREADS; i++) {
        threadParm[i].threadId = i;
        pthread_create(&thread[i], NULL, threadFunc, (void*)&threadParm[i]); 
    }
    for (i=0; i<NUM_THREADS; i++) {
        sem_wait(&sem_parent); 
    }
    fprintf(stdout, "All the child threads has printed.\n");
    for (i=0; i<NUM_THREADS; i++) {
        sem_post(&sem_children);
    }
    for (i=0; i<NUM_THREADS; i++) {
        pthread_join(thread[i], NULL);
    }
    sem_destroy(&sem_parent);
    sem_destroy(&sem_children);
    return 0;
}

障碍

// 初始化
pthread_barrier_t b;
pthread_barrier_init(&b,NULL,3);
// 为等待 barrier，线程应执行
pthread_barrier_wait(&b);

typedef struct {
    int threadId;
} threadParm_t;
pthread_barrier_t barrier;
void *threadFunc(void *parm) {
    threadParm_t *p = (threadParm_t *) parm;
    fprintf(stdout, "Thread %d has entered step 1.\n", p->threadId);
    pthread_barrier_wait(&barrier);
    fprintf(stdout, "Thread %d has entered step 2.\n", p->threadId);
    pthread_exit(NULL);
}
int main(int argc, char *argv[]) {
    pthread_barrier_init(&barrier, NULL, NUM_THREADS);
    pthread_t thread[NUM_THREADS];
    threadParm_t threadParm[NUM_THREADS];
    int i;
    for (i=0; i<NUM_THREADS; i++) {
        threadParm[i].threadId = i;
        pthread_create(&thread[i], NULL, threadFunc, (void*)&threadParm[i]);
    }
    for (i=0; i<NUM_THREADS; i++) {
        pthread_join(thread[i], NULL);
    }
    pthread_barrier_destroy(&barrier);
    system("PAUSE");
    return 0;
}

条件变量

pthread_cond_init(condition,attr);
pthread_cond_destroy(condition);
pthread_condattr_init(attr);
pthread_condattr_destroy (attr);
pthread_cond_wait(condition,mutex); // 条件不成立便阻塞，之前解锁
pthread_cond_signal(condition); // 触发条件，可能唤醒一个阻塞线程
pthread_cond_broadcast(condition); // 唤醒多个线程

#define NUM_THREADS 3
#define TCOUNT 10
#define COUNT_LIMIT 12
int count = 0;
int thread_ids[3] = {0,1,2};
pthread_mutex_t count_mutex;
pthread_cond_t count_threshold_cv;

int main (int argc, char *argv[]) {
    int i, rc;
    pthread_t threads[3];
    pthread_attr_t attr;
    pthread_mutex_init(&count_mutex, NULL);
    pthread_cond_init(&count_threshold_cv, NULL);
    pthread_attr_init(&attr);
    pthread_attr_setdetachstate(&attr, PTHREAD_CREATE_JOINABLE);
    pthread_create(&threads[0], &attr, inc_count, (void *)&thread_ids[0]);
    pthread_create(&threads[1], &attr, inc_count, (void *)&thread_ids[1]);
    pthread_create(&threads[2], &attr, watch_count, (void *)&thread_ids[2]);
    /* Wait for all threads to complete */
    for (i = 0; i < NUM_THREADS; i++) {
        pthread_join(threads[i], NULL);
    }
    printf ("Main(): Waited on %d threads. Done.\n", NUM_THREADS);
    /* Clean up and exit */
    pthread_attr_destroy(&attr);
    pthread_mutex_destroy(&count_mutex);
    pthread_cond_destroy(&count_threshold_cv);
    pthread_exit(NULL);
}

void* inc_count(void* idp) {
    int j, i;
    double result = 0.0;
    int* my_id = idp;
    for (int i = 0; i < T_COUNT; i++) {
        pthread_mutex_lock(&count_mutex);
        count++;
        if (count == COUNT_LIMIT) {
            pthread_cond_singal(&count_threashold_cv);
            printf("inc_count(): thread %d, count = %d Threshold reached.\n", *my_id, count);
        }
        printf("inc_count(): thread %d, count = %d, unlocking mutex\n", *my_id, count);
        pthread_mutex_unlock(&count_mutex);
        for (j = 0; j < 1000; j++)
            reslut = result + (double)rand();
    }
    pthread_exit(NULL);
}

void* watch_count(void* idp) {
    int* my_id = idp;
    printf("Starting watch_count: thread %d\n", *my_id);
    pthread_mutext_lock(&count_mutex);
    while (count < COUNT_LIMIT) {
        pthread_cond_wait(&count_threadshold_cv, &count_mutex);
        printf("watch_count(): thread %d Condition signal received.\n", *my_id);
    }
    pthread_mutex_unlock(&count_mutex);
    pthread_exit(NULL);
}

读写锁

负载均衡&任务划分

一维&二维。

• 循环划分，任务数>线程数，循环分配给线程
• 随机块划分，每个维度随机排列，每个线程任划分一个连续区域

OpenMP 编程

OpenMP 和基础 API

// 返回执行当前并行区域的线程组中的线程数
int omp_get_num_threads(void);
// 返回当前线程在线程组中的编号，值在0 和omp_get_num_threads()-1之间
int omp_get_thread_num(void);

#include <stdio.h>
#include <stdlib.h>
#include <omp.h>
void Trap (double a, double b, int n, double* global_result_p);
int main (int argc, char* argv[]) {
    double global_result = 0.0;
    double a, b;
    int n;
    int thread_count;
    thread_count = strtol(argv[1], NULL, 10);
    printf("Enter a, b, and n\n");
    scanf("%lf %lf %d", &a, &b, &n);
# pragma omp parallel num_threads(thread_count) Trap(a, b, n, &global_result);
    printf("With n = %d trapezoids, our estimate\n", n);
    printf("of the integral from %f to %f = %.14e\n", a, b, global_result);
    return 0;
} /* main*/

void Trap(double a, double b, int n, double* global_result_p) {
    double h, x, my_result;
    double local_a, local_b;
    int i, local_n;
    int my_rank = omp_get_thread_num();
    int thread_count = omp_get_num_threads();
    h = (b-a)/n;
    local_n = n/thread_count;
    local_a = a + my_rank * local_n * h;
    local_b = local_a + local_n * h;
    my_result = (f(local_a) + f(local_b)) / 2.0;
    for (i = 1; i <= local_n; i++) {
        x = local_a + i * h;
        my_result += f(x);
    }
    my_result = my_result * h;
# pragma omp critical
    *global_result_p += my_result ;
} /* Trap*/

规约

归约就是将相同的规约操作符重复地应用到操作数序列来得到一个结果的计算。

sum = 0;
#pragma omp parallel for reduction(+:sum)
for (i=0; i < 100; i++) sum += array[i];

parallel for

• #pragram omp parallel for
• 循环变量：带符号整数
• 终止检测：<，<=，>，>=与循环不变量
• 每步迭代递增、递减一个循环不变量
• 循环体：我进出控制流

/* Input: a, b, n */
h = (b - a) / n;
approx = (f(a) + f(b))/2.0;
#pragma omp parallel for num_threads(thread_count) reduction(+: approx)
for(i = 1; i <= n - 1; i++)
	approx += f(a + i * h);
approx = h * approx;

数据依赖

就是两个内存操作的序，为了保证结果的正确性，必须保持这个序

• 两个计算等价：在相同的输入上，它们产生相同的输出，输出按相同的顺序生成
• 重排转换：改变语句的执行顺序，不增加或删除任何语句的执行
• 一个重排转换保持依赖关系：保持了依赖源和目的语句的相对执行顺序
• 依赖关系基本定理：任何重排转换，只要保持了程序中所有依赖关系，它就保持了程序的含义。

// 循环进位，依赖关系
for (int i = 2; i < 5; i++)
    A[i] = A[i - 2] + 1;

重排转换

• 并行化本质上来说是一种重排转换。要满足并行化操作是重排转换。
• 对于使用满足交换律和结合律的运算的规约操作，对其使用重排是安全的。

double sum = 0.0;
#pragma omp parallel for num_threads(thread_count) reduction(+:sum) private(factor)
for (k = 0; k < n; k++) {
    factor = (k % 2 == 0) ? 1.0 : -1.0;
    sum += factor/(2 * k + 1);
}
pi_approx = 4.0 * sum;

循环调度

• static([chunk]) 静态划分
• dynmaic([chunk]) 动态划分
• guided([chunk]) 动态划分，划分过程中，chunk指数减小

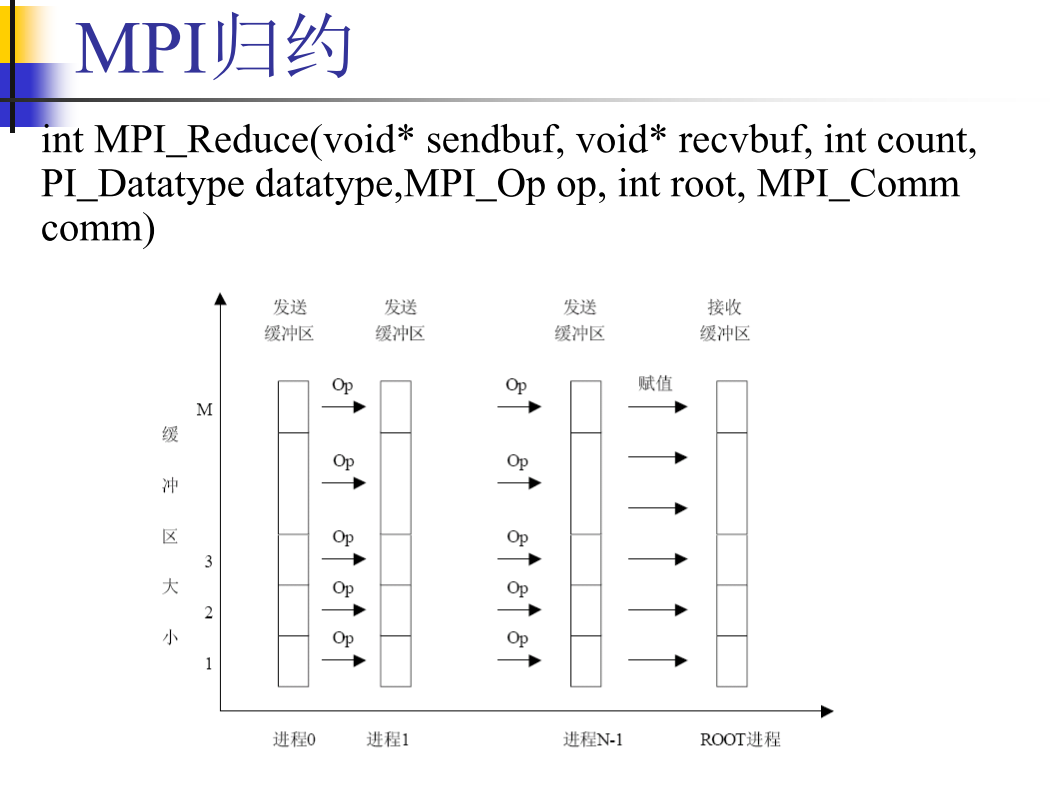
MPI 编程

MPI 原语

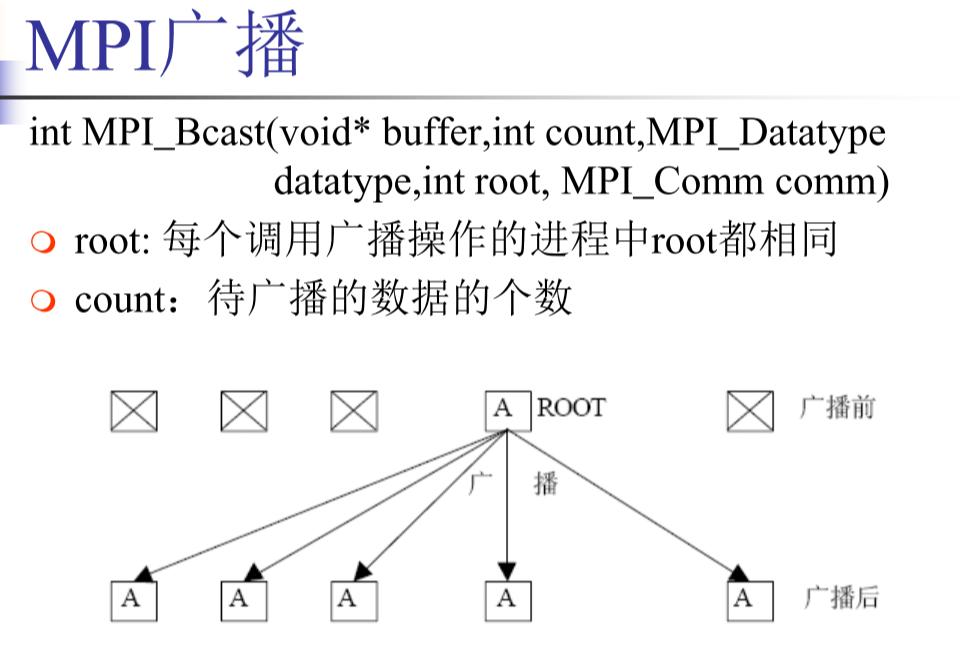
• int MPI_Comm_size(MPI_Comm comm, int* size) 报告进程数
• int MPI_Comm_rank(MPI_Comm comm, int* rank) 报告识别调用进程的rank
• MPI_Init(&argc, &argv)
• MPI_Finalize();

数据类型

MPI_{type}

阻塞通信

• int MPI_Send(void* buf, int count, MPI_Datatype datatype, int dest, int tag, MPI_Comm comm) 发送消息。阻塞发送，函数返回时，数据已经转给系统发送，缓冲区可做他用；但是消息可能未到达目的进程。tag是用户定义整数标签，用来识别消息。
• int MPI_Recv(void* buf, int count ,MPI_Datatype datatype, int source, int tag, MPI_Comm comm, MPI_Status* status) 阻塞接受，

#include <mpi.h>
#include <stdio.h>
int main(int argc, char ** argv) {
    int rank, a[1000], b[500];
    MPI_Init(&argc, &argv);
    MPI_Comm_rank(MPI_COMM_WORLD, &rank);
    if (rank == 0) {
        MPI_Send(&a[500], 500, MPI_INT, 1, 0, MPI_COMM_WORLD);
        sort(a, 500);
        MPI_Recv(b, 500, MPI_INT, 1, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE);
    }
    else if (rank == 1) {
        MPI_Recv(b, 500, MPI_INT, 0, 0, MPI_COMM_WORLD, MPI_STATUS_IGNORE);
        sort(b, 500);
        MPI_Send(b, 500, MPI_INT, 0, 0, MPI_COMM_WORLD);
    }
    MPI_Finalize();
    return 0;
}

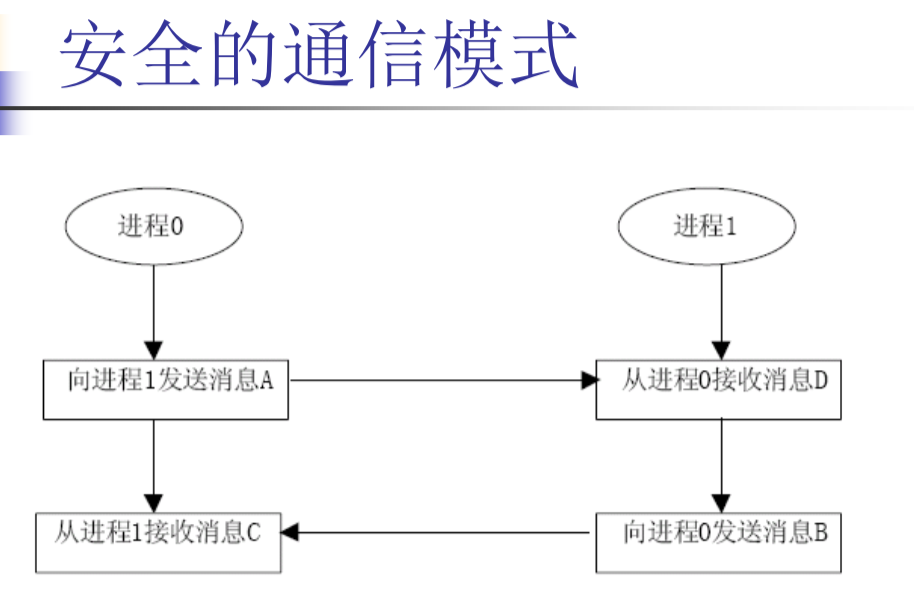
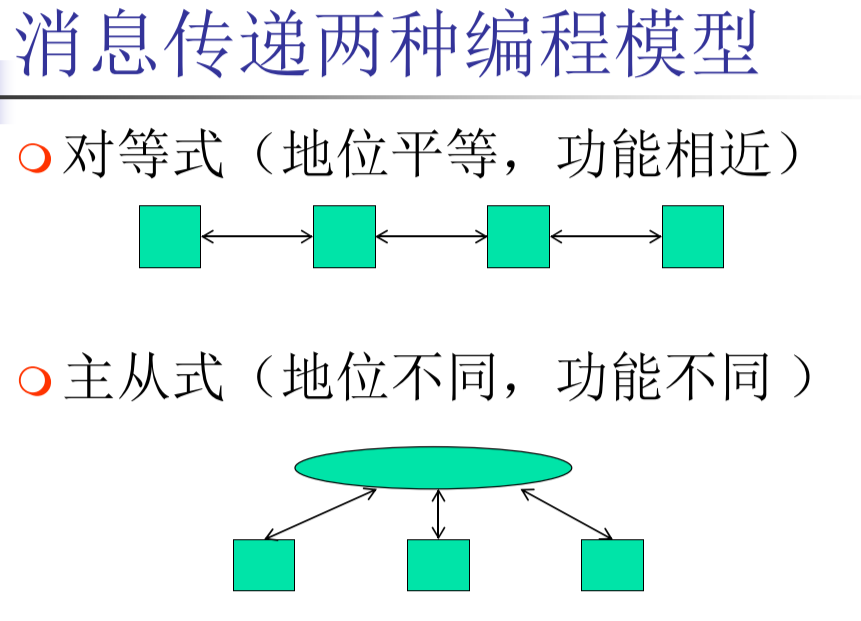
编程模型（对等/主从）

阻塞通信模型

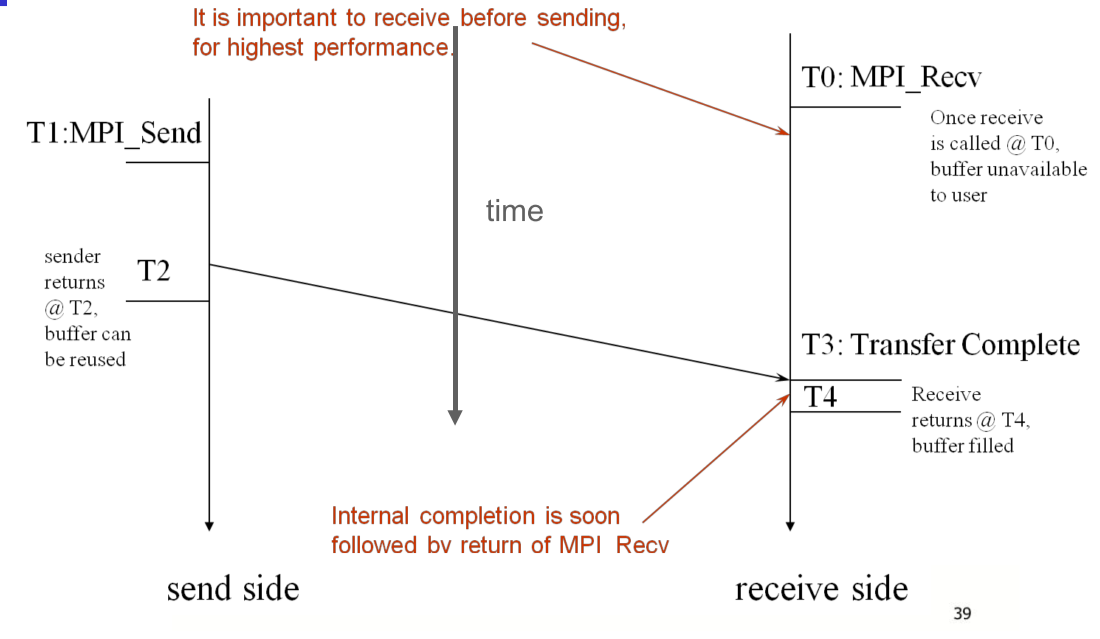
Jacobi 迭代 DEMO

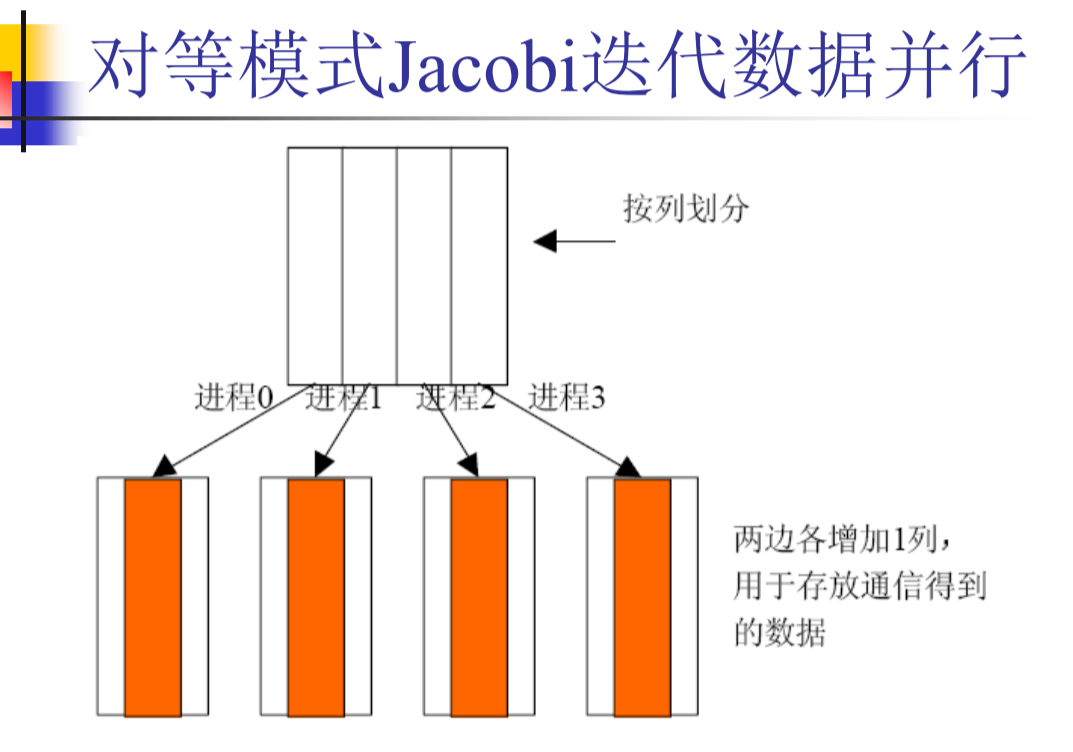
void mpi_jacobi(int rank, int size, int N, int my_n, int steps) {
    for (int k = 0; k < steps; k += 2) {
        if (rank < size - 1)
            // 从下收
            MPI_Recv(&A[my_n + 1], n, MPI_FLOAT, rank + 1, 10, MPI_COMM_WORLD, &status);
        if (rank > 0)
            // 向上发
            MPI_Send(&A[1], n, MPI_FLOAT, rank - 1, 10, MPI_COMM_WORLD);
        if (rank < size - 1)
            // 向下发
            MPI_Send(&A[my_n], n, MPI_FLOAT, rank + 1, 9, MPI_COMM_WORLD);
        if (rank > 0)
            // 从上收
            MPI_Recv(&A[0], n, MPI_FLOAT, rank - 1, 9, MPI_COMM_WORLD, &status);
        for (int i = 1; i <= my_n; i++)
            for (int j = 1; j <= n; j++)
                B[i][j] = 0.25*(A[i - 1][j] + A[i + 1][j] + A[i][j - 1] + A[i][j + 1]);
        if (rank < size - 1)
            MPI_Recv(&B[my_n + 1], n, MPI_FLOAT, rank + 1, 10, MPI_COMM_WORLD, &status);
        if (rank > 0)
            MPI_Send(&B[1], n, MPI_FLOAT, rank - 1, 10, MPI_COMM_WORLD);
        if (rank < size - 1)
            MPI_Send(&B[my_n], n, MPI_FLOAT, rank + 1, 9, MPI_COMM_WORLD);
        if (rank > 0)
            MPI_Recv(&B[0], n, MPI_FLOAT, rank - 1, 9, MPI_COMM_WORLD, &status);
        for (int i = 1; i <= my_n; i++)
            for (int j = 1; j <= n; j++)
                A[i][j] = 0.25*(B[i - 1][j] + B[i + 1][j] + B[i][j - 1] + B[i][j + 1]);
    }
}
if (rank == 0) { 
    init(N);
    QueryPerformanceCounter((LARGE_INTEGER *)&head);
    my_n = N / size;
    for (int i = 1; i < size; i++)
        MPI_Send(&A[i*my_n + 1], N*my_n, MPI_FLOAT, i, 0, MPI_COMM_WORLD);
    mpi_jacobi(rank, size, N, my_n, steps);
    for (int i = 1; i < size; i++)
        MPI_Recv(&A[i*my_n + 1], N*my_n, MPI_FLOAT, i, 1, MPI_COMM_WORLD, &status);
    QueryPerformanceCounter((LARGE_INTEGER *)&tail);
    cout << "MPI: " << (tail - head) * 1000.0 / freq << "ms" << endl;
} else {
    my_n = N / size;
    MPI_Recv(&A[1], N*my_n, MPI_FLOAT, 0, 0, MPI_COMM_WORLD, &status);
    mpi_jacobi(rank, size, N, my_n, steps);
    MPI_Send(&A[1], N*my_n, MPI_FLOAT, 0, 1, MPI_COMM_WORLD);
}

简化通信

MPI_SENDRECV(sendbuf,sendcount,sendtype,dest,sendtag,recvbuf,recvcount,recvtype, source,recvtag,comm,status)

组通信

• 进程可以组成组
• 每个消息都是在一个特定上下文中发送，必须在同一个上下文中接收。
• 进程组和上下文一起形成了通信域
• 进程用它在进程组（与某个通信域关联）中的编号标识
• 在组内通信不需要通信消息标志参数

广播和规约

• one to all broadcast：一个进程向其他所有进程发送相同数据。初始，只有源进程有一份m个字的数据，广播操作后，所有进程都有一份相同数据
• all to one reduction：初始，每个进程都有一份m个字的数据。归约操作后，p份数据经过计算（加、乘、…）得到一份数据（结果），传送到目的进程。
• 矩阵相乘、高斯消去、最短路径、向量内积

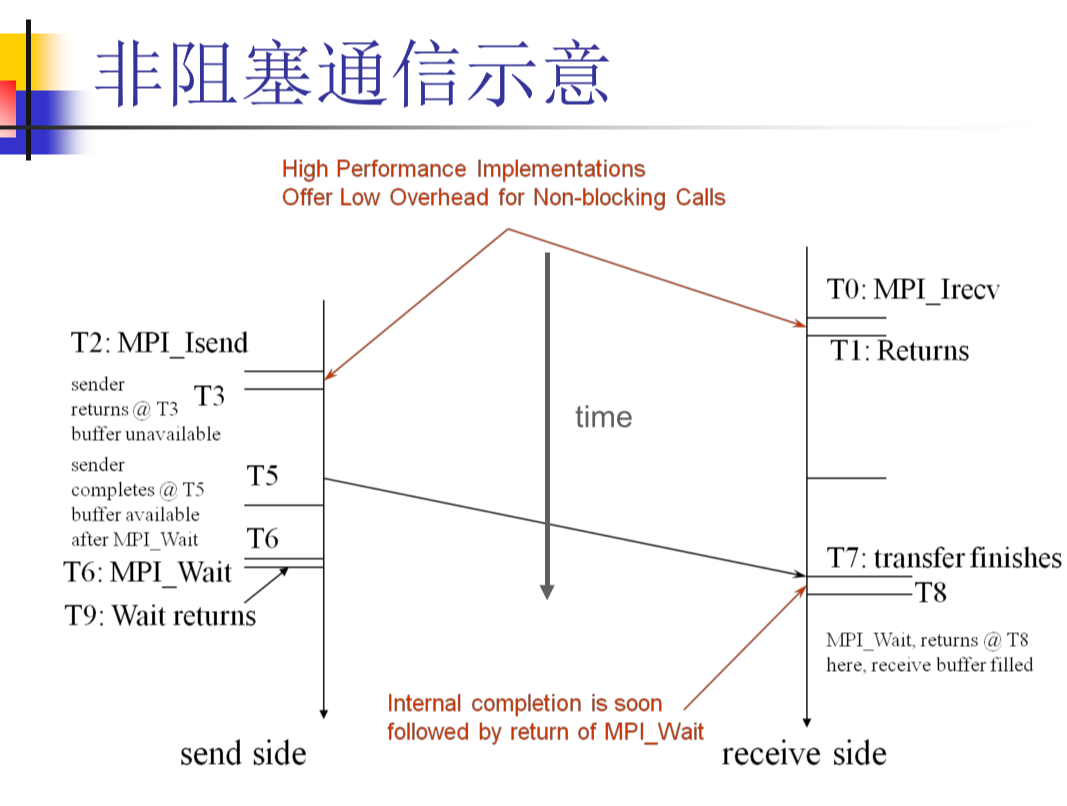
非阻塞通信

混合编程

• Previous
  深度学习的Normalization
• Next
  机器学习总结