介绍
Floyd判圈算法是一种检测图中是否存在环的算法,该算法可以在$O(N)$的时间复杂度,$O(1)$的空间复杂度内完成判断,并且找到环的入口。
算法描述
给定一个图(用链表描述,或者是有向边),图中可能有一个环或没有,给定起始节点,判断图中是否存在环,并且返回环的入口结点。
注意,输入要求从入口一直走下去,不会出现多叉路口。
-
设置两个指针(快指针和慢指针),让这两个指针指向图的入口。快指针循环一次移动两个节点,慢指针移动一个节点。如果图存在环,那么必然会在环中的某个位置相遇,记录这个位置,执行2。如果不存在环,快指针则会在$O(N/2)$的时间内到达不能向下移动的位置,算法结束。
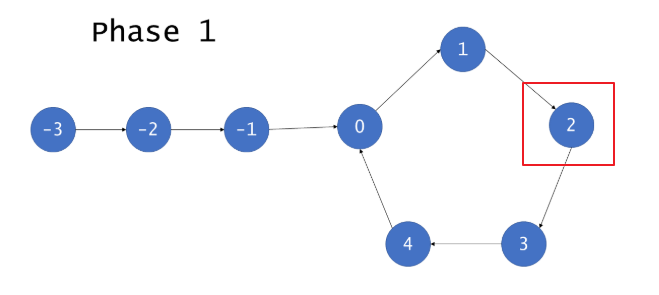
-
重新标记两个新指针,分别指向起始位置和标记的相遇位置,让这两个指针同步向后遍历,它们相遇的位置即为图中环的入口。
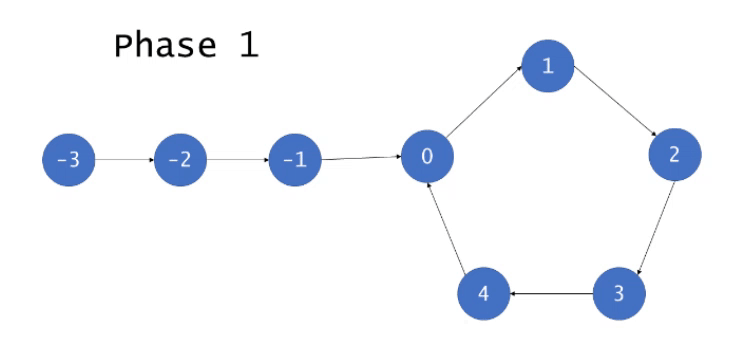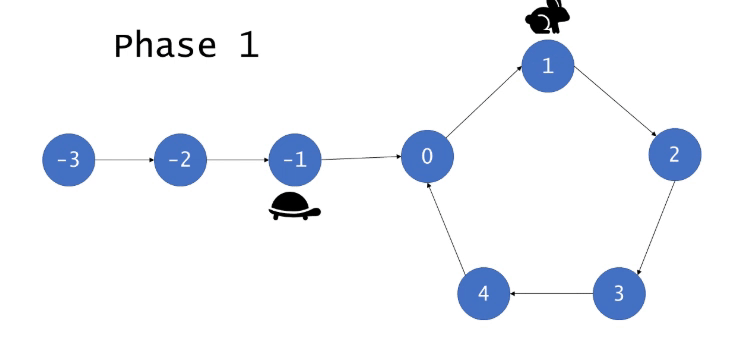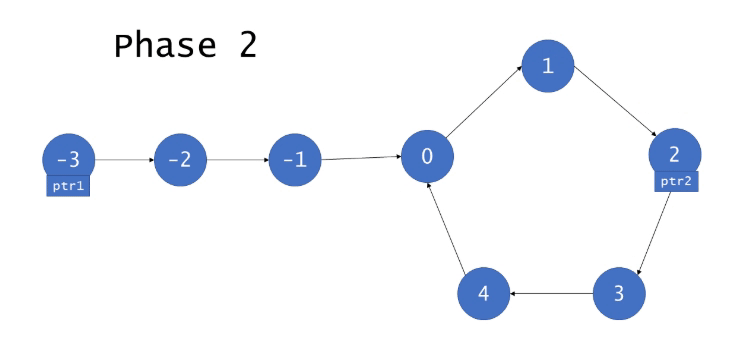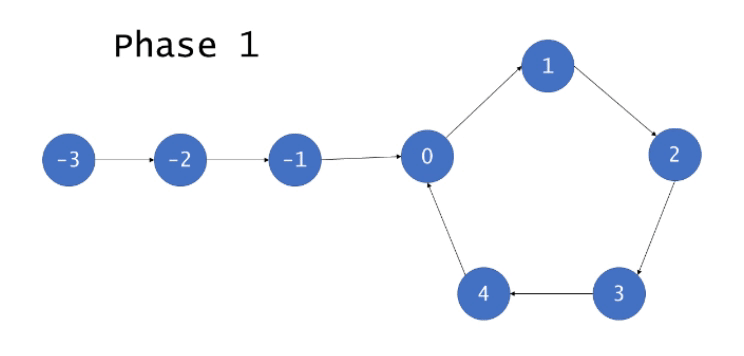
算法证明
我们约定从图的入口到环的入口之前共有$F$个节点,编号为$-F\sim-1$,约定图中的环的部分共有$N$个节点,编号为$0\sim N-1$。
对于阶段1,由于图中存在环,那么很直观,快慢指针都会进入环,由于两指针一个速度为1,一个速度为2,那么两个指针最终会在环中某个位置相遇。
将阶段1分为两部分看待,前$F$次迭代中,慢指针移动$F$次,恰好指向节点$0$,快指针移动$2F$次,指向环内某个节点$h$,其中$F\equiv h(mod\text{ }N)$,即$F$与$h$同余。继续迭代$N-h$次,慢指针显然会指向$C-h$节点,我们来分析快指针:
\[h+2(N-h)=2N-h\\ 2N-h\equiv N-h(mod \text{ } N)\]即快指针最终也会指向$C-h$节点。
对阶段2,如下图所示,我们需要证明$F=b$即可。 需要注意的是,对于节点h,是我们利用快慢指针不同速度一定会相遇的条件得到的。那么对于快慢指针的路程有一个二倍关系,即:
\[F+a+b+a=2(F+a)\\ F=b\]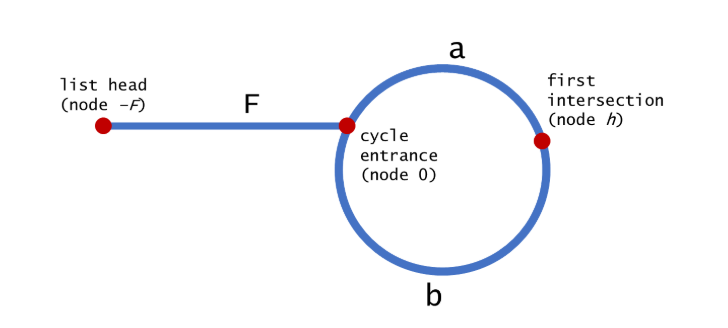
至此,理论证明完毕。
例子
Code:
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode* faster = head;
ListNode* slower = head;
ListNode* target = NULL;
while (faster && faster->next) {
faster = faster->next->next;
slower = slower->next;
if (faster == slower) {
target = faster;
break;
}
}
if (target == NULL) return NULL;
ListNode* ptr1 = head, *ptr2 = target;
while (ptr1 != ptr2) {
ptr1 = ptr1->next;
ptr2 = ptr2->next;
}
return ptr1;
}
};